题目内容
20.若方程组$\left\{\begin{array}{l}{{y}^{2}-4x-2y+1=0}\\{y=x+m}\end{array}\right.$无实数解,求m的取值范围.分析 把②代入①得出x2+(2m-6)x+(m2-2m+1)=0,根据方程组无实数解得出△<0,推出(2m-6)2-4(m2-2m+1)<0,求出不等式的解集即可.
解答 解:$\left\{\begin{array}{l}{{y}^{2}-4x-2y+1=0①}\\{y=x+m②}\end{array}\right.$
把②代入①得:(x+m)2-4x-2(x+m)+1=0,
x2+(2m-6)x+(m2-2m+1)=0,
∵方程组$\left\{\begin{array}{l}{{y}^{2}-4x-2y+1=0}\\{y=x+m}\end{array}\right.$无实数解,
∴△<0,
∴(2m-6)2-4(m2-2m+1)<0,
解得:m>2,
即m的取值范围是m>2.
点评 本题考查了高次方程组,根的判别式的应用,能把方程组转化成一元二次方程是解此题的关键.

练习册系列答案
相关题目
12.已知a2(b+c)=b2(a+c)=2015,且a,b,c互不相等,则c2(a+b)-2014的值为( )
| A. | 0 | B. | 1 | C. | 2015 | D. | -2015 |
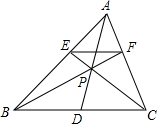 如图,△ABC中,E、F在AB、AC上,EF∥BC,BF、CE交于点P,延长AP交BC于点D,求证:BD=CD.
如图,△ABC中,E、F在AB、AC上,EF∥BC,BF、CE交于点P,延长AP交BC于点D,求证:BD=CD.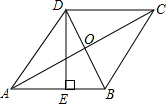 如图,在菱形ABCD中,DE=AO,DE⊥AB,AB=2.
如图,在菱形ABCD中,DE=AO,DE⊥AB,AB=2. 如图,在?ABCD中,AE=CF,试说明EF,BD互相平分的理由.
如图,在?ABCD中,AE=CF,试说明EF,BD互相平分的理由.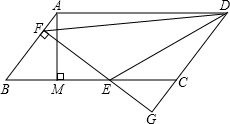 如图,平行四边形ABCD中,AB=5,BC=10,BC边上的高AM=4,E为BC边上的一个动点(不与B、C重合).过E作直线AB的垂线,垂足为F.FE与DC的延长线相交于点G,当点E在线段BC上运动时,△BEF和△CEG的周长之和是不是定值?如果是定值,求出这个值;如果不是,请说明你的理由.
如图,平行四边形ABCD中,AB=5,BC=10,BC边上的高AM=4,E为BC边上的一个动点(不与B、C重合).过E作直线AB的垂线,垂足为F.FE与DC的延长线相交于点G,当点E在线段BC上运动时,△BEF和△CEG的周长之和是不是定值?如果是定值,求出这个值;如果不是,请说明你的理由.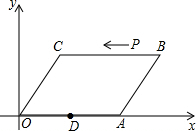 如图,在平面直角坐标系中,?OABC的顶点A,C的坐标分别为(10,0),(2,4),点D是OA的中点,点P在BC上由点B向点C运动,速度为2cm/s
如图,在平面直角坐标系中,?OABC的顶点A,C的坐标分别为(10,0),(2,4),点D是OA的中点,点P在BC上由点B向点C运动,速度为2cm/s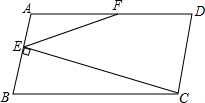 如图,?ABCD中,E为AB的中点,F为AD的中点,且CE⊥AB,若AB=4,CE=8,则EF的长为5.
如图,?ABCD中,E为AB的中点,F为AD的中点,且CE⊥AB,若AB=4,CE=8,则EF的长为5.