题目内容
15.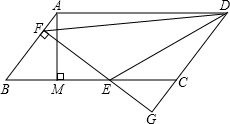 如图,平行四边形ABCD中,AB=5,BC=10,BC边上的高AM=4,E为BC边上的一个动点(不与B、C重合).过E作直线AB的垂线,垂足为F.FE与DC的延长线相交于点G,当点E在线段BC上运动时,△BEF和△CEG的周长之和是不是定值?如果是定值,求出这个值;如果不是,请说明你的理由.
如图,平行四边形ABCD中,AB=5,BC=10,BC边上的高AM=4,E为BC边上的一个动点(不与B、C重合).过E作直线AB的垂线,垂足为F.FE与DC的延长线相交于点G,当点E在线段BC上运动时,△BEF和△CEG的周长之和是不是定值?如果是定值,求出这个值;如果不是,请说明你的理由.
分析 过点C作FG的平行线交直线AB于H,证得四边形FHCG为矩形.得出FH=CG,FG=CH,所以△BEF与△CEG的周长之和等于BC+CH+BH,证得Rt△BEF∽Rt△BAM,那么根据相似三角形的性质得到$\frac{AB}{BC}=\frac{AM}{CH}$,即可求得CH=8,然后根据勾股定理求得BH=6,即可求出两三角形的周长和是24.
解答 解:是定值,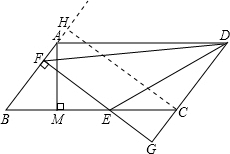 过点C作FG的平行线交直线AB于H,
过点C作FG的平行线交直线AB于H,
因为GF⊥AB,所以四边形FHCG为矩形.
所以FH=CG,FG=CH,
因此,△BEF与△CEG的周长之和等于BC+CH+BH,
∵∠B=∠B,∠AMB=∠BHC=90°
∴△ABM∽△CBH,
∴$\frac{AB}{BC}=\frac{AM}{CH}$,
由BC=10,AB=5,AM=4,
∴CH=$\frac{AM•BC}{AB}$=$\frac{4×10}{5}$=8,
在RT△BCH中,BH=$\sqrt{B{C}^{2}-C{H}^{2}}$=6,
所以BC+CH+BH=24,
所以,△BEF与△CEG的周长之和为24是定值.
点评 此题主要考查了矩形的判定和性质,相似三角形的判定和性质,勾股定理,熟练掌握相似三角形的判定与性质是解题关键.

练习册系列答案
 课堂全解字词句段篇章系列答案
课堂全解字词句段篇章系列答案 步步高口算题卡系列答案
步步高口算题卡系列答案 点睛新教材全能解读系列答案
点睛新教材全能解读系列答案 小学教材完全解读系列答案
小学教材完全解读系列答案
相关题目
5.菱形中某两个角的和是90°,周长是12,则菱形的面积是( )
| A. | $\frac{3\sqrt{2}}{2}$ | B. | $\frac{5\sqrt{2}}{2}$ | C. | $\frac{7\sqrt{2}}{2}$ | D. | $\frac{9\sqrt{2}}{2}$ |
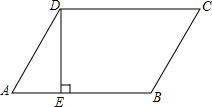 如图,在平行四边形ABCD中,AD=BC,AB=CD,DE⊥AB于点E,∠A=60°,BE=2AE=$\sqrt{72}$cm,求平行四边形ABCD的周长.
如图,在平行四边形ABCD中,AD=BC,AB=CD,DE⊥AB于点E,∠A=60°,BE=2AE=$\sqrt{72}$cm,求平行四边形ABCD的周长.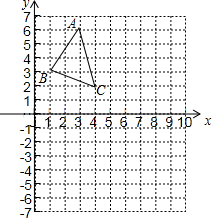 如图,△ABC的顶点坐标分别是A(3,6)、B(1,3)、C(4,2).
如图,△ABC的顶点坐标分别是A(3,6)、B(1,3)、C(4,2). 将一个宽度相等的纸条如图所示折叠一下,那么∠2=50°,∠1=65°.
将一个宽度相等的纸条如图所示折叠一下,那么∠2=50°,∠1=65°.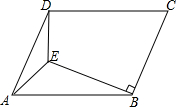 如图,E是?ABCD内一点,ED⊥CD,EB⊥BC,∠AED=135°,连CE交AD于F.
如图,E是?ABCD内一点,ED⊥CD,EB⊥BC,∠AED=135°,连CE交AD于F.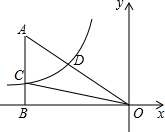 如图,已知双曲线y=$\frac{k}{x}$(k<0)经过直角三角形OAB斜边OA的中点D,且与直角边AB相交于点C.若点A的坐标为(-8,6),则△AOC的面积为18.
如图,已知双曲线y=$\frac{k}{x}$(k<0)经过直角三角形OAB斜边OA的中点D,且与直角边AB相交于点C.若点A的坐标为(-8,6),则△AOC的面积为18.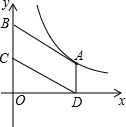 如图,在平面直角坐标系中,?ABCD的顶点A在函数y=$\frac{k}{x}(k>0,x>0)$的图象上,顶点B、C在y轴正半轴上(点B在点C的上方),若点D的坐标为(3,0),?ABCD的面积为4.5,则k的值为4.5.
如图,在平面直角坐标系中,?ABCD的顶点A在函数y=$\frac{k}{x}(k>0,x>0)$的图象上,顶点B、C在y轴正半轴上(点B在点C的上方),若点D的坐标为(3,0),?ABCD的面积为4.5,则k的值为4.5.