题目内容
15. 如图,正方形ABCD中,AB=3$\sqrt{10}$,E为对角线BD上一点,DE=2$\sqrt{5}$,EF⊥BD,交DC于点F,M为BD中点,将△DEF绕着D点顺时针旋转得到△DNH,连接BH,当BH恰好经过F点时,取BH的中点G,连接GN、MG,则四边形DMGN的面积为$\frac{29}{2}$.
如图,正方形ABCD中,AB=3$\sqrt{10}$,E为对角线BD上一点,DE=2$\sqrt{5}$,EF⊥BD,交DC于点F,M为BD中点,将△DEF绕着D点顺时针旋转得到△DNH,连接BH,当BH恰好经过F点时,取BH的中点G,连接GN、MG,则四边形DMGN的面积为$\frac{29}{2}$.
分析 取FH的中点P,过N作NQ⊥DP于Q,连接NP,NF,根据相似三角形的性质得到FP=2,DP=6,于是得到FH=2FP=4,BH=14,BP=12,推出D,N,P,H四点共圆,根据圆周角定理得到∠NDP=∠NHF,∠DPN=∠DHN=45°,设PQ=x,则DQ=6-x,NQ=x,根据勾股定理得到QN=2=FP,推出四边形NQPF是正方形,∴求得S△BDH=$\frac{1}{2}$BH•DP=42,S△NGH=$\frac{1}{2}$GH•NF=7,根据三角形的中位线的性质得到MG=$\frac{1}{2}$DH,MG∥DH,于是得到结论.
解答  解:取FH的中点P,过N作NQ⊥DP于Q,连接NP,NF,
解:取FH的中点P,过N作NQ⊥DP于Q,连接NP,NF,
∴DP⊥FH,
∴△DFP∽△BFC,
∴$\frac{FP}{FC}=\frac{DP}{BC}=\frac{DF}{BF}$,
∵DF=$\sqrt{2}$DE=2$\sqrt{10}$,
∴CF=CD-DF=$\sqrt{10}$,
∵BF=$\sqrt{C{F}^{2}+B{C}^{2}}$=10,
∴$\frac{PF}{\sqrt{10}}=\frac{DP}{3\sqrt{10}}=\frac{2\sqrt{10}}{10}$,
∴FP=2,DP=6,
∴FH=2FP=4,BH=14,BP=12,
∵∠DNH=90°=∠DPH,
∴D,N,P,H四点共圆,
∴∠NDP=∠NHF,∠DPN=∠DHN=45°,
∴NQ=PQ,
设PQ=x,则DQ=6-x,NQ=x,
在Rt△DNQ中,DN2=DQ2+NQ2,
∴(2$\sqrt{5}$)2=(6-x)2+x2,
解得:x=2,或x=4(舍去),
∴QN=2=FP,
∵NQ∥DP,FP⊥DP,
∴四边形NQPF是正方形,
∴NF∥PQ,NF⊥BH,
∴S△BDH=$\frac{1}{2}$BH•DP=42,S△NGH=$\frac{1}{2}$GH•NF=7,
∵G是BH的中点,M为BD中点,
∴MG=$\frac{1}{2}$DH,MG∥DH,
∴S△BMG=$\frac{1}{4}$S△BDH=$\frac{21}{2}$,
∵S△NDH=$\frac{1}{2}$DN•NH=10,
∴四边形DMGN的面积=S△BDH-S△BMG-S△NDH-S△NGH=$\frac{29}{2}$.
故答案为:$\frac{29}{2}$.
点评 本题考查了旋转的性质,正方形的性质,三角形的中位线的性质,勾股定理,相似三角形的判定和性质,正确的作出辅助线是解题的关键.

 应用题作业本系列答案
应用题作业本系列答案| A. | 2:3 | B. | 8:5 | C. | 10:1 | D. | 5:8 |
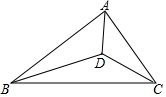 如图,直角三角形ABC中,∠BAC=90°,点D为三角形内部一点,连接AD,BD.CD,AD平分∠BAC,∠BDC=135°,AD=2$\sqrt{2}$,BD=$\sqrt{2}$CD,则BC的长为( )
如图,直角三角形ABC中,∠BAC=90°,点D为三角形内部一点,连接AD,BD.CD,AD平分∠BAC,∠BDC=135°,AD=2$\sqrt{2}$,BD=$\sqrt{2}$CD,则BC的长为( )| A. | 6 | B. | 8 | C. | 10 | D. | 12 |
| A. | $\sqrt{-x-2}$ | B. | $\sqrt{x}$ | C. | $\sqrt{{x}^{2}+2}$ | D. | $\sqrt{-5}$ |
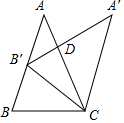 如图,在△ABC中,AB=AC,将△ABC绕点C顺时针旋转后得到△A'B'C,设∠A'CB=a,点B'在AB上,则∠ADA'=4α-360°(用含a的式子表示)
如图,在△ABC中,AB=AC,将△ABC绕点C顺时针旋转后得到△A'B'C,设∠A'CB=a,点B'在AB上,则∠ADA'=4α-360°(用含a的式子表示)