题目内容
10.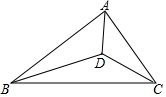 如图,直角三角形ABC中,∠BAC=90°,点D为三角形内部一点,连接AD,BD.CD,AD平分∠BAC,∠BDC=135°,AD=2$\sqrt{2}$,BD=$\sqrt{2}$CD,则BC的长为( )
如图,直角三角形ABC中,∠BAC=90°,点D为三角形内部一点,连接AD,BD.CD,AD平分∠BAC,∠BDC=135°,AD=2$\sqrt{2}$,BD=$\sqrt{2}$CD,则BC的长为( )| A. | 6 | B. | 8 | C. | 10 | D. | 12 |
分析 根据题意可以作出合适的辅助线,然后根据等腰三角形的性质和三角形的相似可以求得AB和AC的长,再根据勾股定理即可求得BC的长.
解答  解:过点D作EF⊥AD于点D,交AB于点E,交AC于点F,
解:过点D作EF⊥AD于点D,交AB于点E,交AC于点F,
∵∠BAC=90°,AD平分∠BAC,
∴∠AED=∠AFD=∠EAD=∠FAD=45°,
∴AD=DE=DF,
∵AD=2$\sqrt{2}$,
∴DE=DF=2$\sqrt{2}$,AE=AF=4,
∵∠AED=∠AFD=45°,∠BDC=135°,
∴∠EBD+∠EDB=45°,∠EDB+∠FDC=45°,∠FDC+∠FCD=45°,
∴∠EBD=∠FDC,∠EDB=∠FCD,
∴△EDB∽△FCD,
∴$\frac{ED}{FC}=\frac{EB}{FD}=\frac{BD}{DC}$,
∵BD=$\sqrt{2}$CD,ED=FD=2$\sqrt{2}$,
∴$\frac{2\sqrt{2}}{FC}=\frac{EB}{2\sqrt{2}}=\sqrt{2}$,
解得,FC=2,EB=4,
∴AB=AE+BE=8,AC=AF+FC=6,
∴BC=$\sqrt{{8}^{2}+{6}^{2}}=10$,
故选C.
点评 本题考查勾股定理,解答本题的关键是明确题意,求出边AB和AC的长,利用勾股定理和三角形的相似解答.

练习册系列答案
 一线名师权威作业本系列答案
一线名师权威作业本系列答案
相关题目
1.一个数的倒数是它的本身,这个数是( )
| A. | 0 | B. | 1 | C. | -1 | D. | 1或-1 |
18.若|a|=5,|b|=7且|a+b|=a+b,则a-b的值为( )
| A. | 2或-2 | B. | 12或-12 | C. | -2或-12 | D. | 5或7 |
5. 如图是婴儿车的平面示意图,其中AB∥CD,∠1=124°,∠3=40°,那么∠2的度数为( )
如图是婴儿车的平面示意图,其中AB∥CD,∠1=124°,∠3=40°,那么∠2的度数为( )
 如图是婴儿车的平面示意图,其中AB∥CD,∠1=124°,∠3=40°,那么∠2的度数为( )
如图是婴儿车的平面示意图,其中AB∥CD,∠1=124°,∠3=40°,那么∠2的度数为( )| A. | 74° | B. | 76° | C. | 84° | D. | 86° |
 如图,正方形ABCD中,AB=3$\sqrt{10}$,E为对角线BD上一点,DE=2$\sqrt{5}$,EF⊥BD,交DC于点F,M为BD中点,将△DEF绕着D点顺时针旋转得到△DNH,连接BH,当BH恰好经过F点时,取BH的中点G,连接GN、MG,则四边形DMGN的面积为$\frac{29}{2}$.
如图,正方形ABCD中,AB=3$\sqrt{10}$,E为对角线BD上一点,DE=2$\sqrt{5}$,EF⊥BD,交DC于点F,M为BD中点,将△DEF绕着D点顺时针旋转得到△DNH,连接BH,当BH恰好经过F点时,取BH的中点G,连接GN、MG,则四边形DMGN的面积为$\frac{29}{2}$.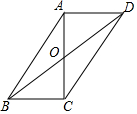 如图,在?ABCD中,对角线AC,BD交于点O,AC⊥BC,若$\frac{BD}{CD}$=$\frac{8}{5}$,则$\frac{BC}{AC}$=$\frac{\sqrt{39}}{6}$.
如图,在?ABCD中,对角线AC,BD交于点O,AC⊥BC,若$\frac{BD}{CD}$=$\frac{8}{5}$,则$\frac{BC}{AC}$=$\frac{\sqrt{39}}{6}$.