题目内容
7.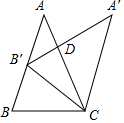 如图,在△ABC中,AB=AC,将△ABC绕点C顺时针旋转后得到△A'B'C,设∠A'CB=a,点B'在AB上,则∠ADA'=4α-360°(用含a的式子表示)
如图,在△ABC中,AB=AC,将△ABC绕点C顺时针旋转后得到△A'B'C,设∠A'CB=a,点B'在AB上,则∠ADA'=4α-360°(用含a的式子表示)
分析 设∠B=x,根据旋转的性质得到∠BB′C=∠A′B′C=∠A′CB′=x,于是得到∠BCB′=180°-2x=∠A=∠A′,求得∠BCB′=α-x,等量代换得到α-x=180°-2x,求得x=180°-α推出∠A′CA=2α-180°,于是得到结论.
解答 解:设∠B=x,
∵将△ABC绕点C顺时针旋转后得到△A'B'C,
∴∠BB′C=∠A′B′C=∠A′CB′=x,
∴∠BCB′=180°-2x=∠A=∠A′,
∵∠A'CB=a,
∴∠BCB′=α-x,
∴α-x=180°-2x,
∴x=180°-α,
∴∠BCB′=α-(180°-α)=2α-180°,
∴∠A′CA=2α-180°,
∴∠ADA′=∠A′+∠A′CA=180°-2x+2α180°=4α-360°.
故答案为:4α-360°.
点评 此题考查了旋转的性质和等腰三角形的性质,解本题的关键是用等腰三角形进行计算.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
18.若|a|=5,|b|=7且|a+b|=a+b,则a-b的值为( )
| A. | 2或-2 | B. | 12或-12 | C. | -2或-12 | D. | 5或7 |
17.计算:$\frac{{x}^{2}-x}{x}÷\frac{1-x}{2x}$=( )
| A. | -2x | B. | 2x | C. | -x | D. | x |
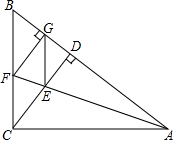 如图,在Rt△ABC中,∠ACB=90°,CD为AB边上的高,∠CAB的平分线交CD于点E,交CB于点F,过点F作FG⊥AB于点G,连接GE.求证:四边形CEGF是菱形.
如图,在Rt△ABC中,∠ACB=90°,CD为AB边上的高,∠CAB的平分线交CD于点E,交CB于点F,过点F作FG⊥AB于点G,连接GE.求证:四边形CEGF是菱形. 如图,正方形ABCD中,AB=3$\sqrt{10}$,E为对角线BD上一点,DE=2$\sqrt{5}$,EF⊥BD,交DC于点F,M为BD中点,将△DEF绕着D点顺时针旋转得到△DNH,连接BH,当BH恰好经过F点时,取BH的中点G,连接GN、MG,则四边形DMGN的面积为$\frac{29}{2}$.
如图,正方形ABCD中,AB=3$\sqrt{10}$,E为对角线BD上一点,DE=2$\sqrt{5}$,EF⊥BD,交DC于点F,M为BD中点,将△DEF绕着D点顺时针旋转得到△DNH,连接BH,当BH恰好经过F点时,取BH的中点G,连接GN、MG,则四边形DMGN的面积为$\frac{29}{2}$.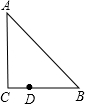 Rt△ABC中,已知∠C=90°,点D在边BC上,BD=2CD(如图),把线段BD绕着点D逆时针旋转m(0<m<180°)后,使得点B恰好落在边AC上,那么m=120°.
Rt△ABC中,已知∠C=90°,点D在边BC上,BD=2CD(如图),把线段BD绕着点D逆时针旋转m(0<m<180°)后,使得点B恰好落在边AC上,那么m=120°.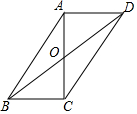 如图,在?ABCD中,对角线AC,BD交于点O,AC⊥BC,若$\frac{BD}{CD}$=$\frac{8}{5}$,则$\frac{BC}{AC}$=$\frac{\sqrt{39}}{6}$.
如图,在?ABCD中,对角线AC,BD交于点O,AC⊥BC,若$\frac{BD}{CD}$=$\frac{8}{5}$,则$\frac{BC}{AC}$=$\frac{\sqrt{39}}{6}$.