题目内容
20.已知,在Rt△ABC中,∠C=90°,AB=13,BC=5,且点D,点G分别是内心和重心,则DG=$\frac{13}{6}$.分析 首先判定D是AB的中点,再根据直角三角形斜边上的中线等于斜边的一半可得CD=$\frac{13}{2}$,最后根据重心的性质可求DG.
解答  解:∵∠C=90°,点D是Rt△ABC的内心,
解:∵∠C=90°,点D是Rt△ABC的内心,
∴D是AB的中点,
∵AB=13,CD为AB边上的中线,
∴CD=13÷2=$\frac{13}{2}$,
∵点G是重心,
∴DG=$\frac{1}{3}$CD=$\frac{13}{6}$.
故答案为:$\frac{13}{6}$.
点评 此题主要考查重心的性质:三角形的重心到顶点的距离是它到对边中点的距离的2倍,综合利用了勾股定理和直角三角形的性质.

练习册系列答案
相关题目
5.下列方程中,有实根的是( )
| A. | $\sqrt{x+1}+\sqrt{x+2}+3=0$ | B. | $\sqrt{x-9}+\sqrt{4-x}=16$ | ||
| C. | $\sqrt{{x}^{2}+1}-\sqrt{{x}^{2}+2}=1-\frac{1}{\sqrt{{x}^{2}+1}}$ | D. | 6$\sqrt{{x}^{2}-2x+6}=21+2x-{x}^{2}$ |
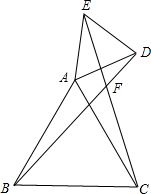 已知:如图所示,△ABC与△ADE均为等边三角形,点A为它们公共顶点,现连接BD、EC,BD与EC交于F点:
已知:如图所示,△ABC与△ADE均为等边三角形,点A为它们公共顶点,现连接BD、EC,BD与EC交于F点: 如图,正方形ABCD中,AB=3$\sqrt{10}$,E为对角线BD上一点,DE=2$\sqrt{5}$,EF⊥BD,交DC于点F,M为BD中点,将△DEF绕着D点顺时针旋转得到△DNH,连接BH,当BH恰好经过F点时,取BH的中点G,连接GN、MG,则四边形DMGN的面积为$\frac{29}{2}$.
如图,正方形ABCD中,AB=3$\sqrt{10}$,E为对角线BD上一点,DE=2$\sqrt{5}$,EF⊥BD,交DC于点F,M为BD中点,将△DEF绕着D点顺时针旋转得到△DNH,连接BH,当BH恰好经过F点时,取BH的中点G,连接GN、MG,则四边形DMGN的面积为$\frac{29}{2}$.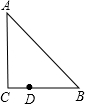 Rt△ABC中,已知∠C=90°,点D在边BC上,BD=2CD(如图),把线段BD绕着点D逆时针旋转m(0<m<180°)后,使得点B恰好落在边AC上,那么m=120°.
Rt△ABC中,已知∠C=90°,点D在边BC上,BD=2CD(如图),把线段BD绕着点D逆时针旋转m(0<m<180°)后,使得点B恰好落在边AC上,那么m=120°.