题目内容
9.已知a,b为定值,关于x的方程$\frac{kx+a}{3}$=1-$\frac{2x+bk}{6}$,无论k为何值,它的解总是1,则a+b=0.分析 把x=1代入方程$\frac{kx+a}{3}$=1-$\frac{2x+bk}{6}$,得:$\frac{k+a}{3}$=1-$\frac{2+bk}{6}$,整理可得(2+b)k+2a-4=0,再根据题意可得2+b=0,2a-4=0,进而可得a、b的值,从而可得答案.
解答 解:把x=1代入方程$\frac{kx+a}{3}$=1-$\frac{2x+bk}{6}$,得:
$\frac{k+a}{3}$=1-$\frac{2+bk}{6}$,
2(k+a)=6-(2+bk),
2k+2a=6-2-bk,
2k+bk+2a-4=0,
(2+b)k+2a-4=0,
∵无论k为何值,它的解总是1,
∴2+b=0,2a-4=0,
解得:b=-2,a=2.
则a+b=0.
故答案为:0.
点评 本题主要考查方程解的定义,由k可以取任何值得到a和b的值是解题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
1. 如图,A,B,C,D是⊙O的四等分点,点P是劣弧$\widehat{AB}$上的动点,当点P从点A向点B运动时(点P不与A、B重合).若⊙O的半径为2.则图中阴影部分面积的最大值是( )
如图,A,B,C,D是⊙O的四等分点,点P是劣弧$\widehat{AB}$上的动点,当点P从点A向点B运动时(点P不与A、B重合).若⊙O的半径为2.则图中阴影部分面积的最大值是( )
 如图,A,B,C,D是⊙O的四等分点,点P是劣弧$\widehat{AB}$上的动点,当点P从点A向点B运动时(点P不与A、B重合).若⊙O的半径为2.则图中阴影部分面积的最大值是( )
如图,A,B,C,D是⊙O的四等分点,点P是劣弧$\widehat{AB}$上的动点,当点P从点A向点B运动时(点P不与A、B重合).若⊙O的半径为2.则图中阴影部分面积的最大值是( )| A. | $\sqrt{2}$ | B. | 2 | C. | 2$\sqrt{2}$ | D. | 2$\sqrt{2}$+2 |
18.下面各组数是三角形的三边的长,则能构成直角三角形的是( )
| A. | 2,2,3 | B. | 6,8,10 | C. | 4,5,6 | D. | 5,6,7 |
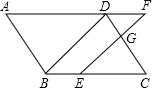 如图,在平行四边形ABCD中,点E在边BC上,点F在边AD的延长线上,且DF=BE,EF与CD交于点G.
如图,在平行四边形ABCD中,点E在边BC上,点F在边AD的延长线上,且DF=BE,EF与CD交于点G.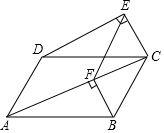 如图,已知四边形ABCD是平行四边形,∠EDC=∠CAB,∠DEC=90°.
如图,已知四边形ABCD是平行四边形,∠EDC=∠CAB,∠DEC=90°.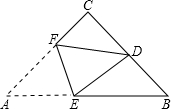 如图,在等腰Rt△ABC中,∠C=90°,D是BC的中点,将△ABC折叠,使A点与D点重合,EF为折痕.
如图,在等腰Rt△ABC中,∠C=90°,D是BC的中点,将△ABC折叠,使A点与D点重合,EF为折痕.