题目内容
18．下面各组数是三角形的三边的长，则能构成直角三角形的是（ ）| A． | 2，2，3 | B． | 6，8，10 | C． | 4，5，6 | D． | 5，6，7 |
分析 欲求证是否为直角三角形，这里给出三边的长，只要验证两小边的平方和等于最长边的平方即可．
解答 解：A、22+22≠32，故不能构成直角三角形；
B、62+82=102，故能构成直角三角形；
C、42+52≠62，故不能构成直角三角形；
D、52+62≠72，故不能构成直角三角形．
故选B．
点评 本题考查勾股定理的逆定理的应用．判断三角形是否为直角三角形，已知三角形三边的长，只要利用勾股定理的逆定理加以判断即可．勾股定理的逆定理：若三角形三边满足a2+b2=c2，那么这个三角形是直角三角形．
练习册系列答案
相关题目
1．一张方桌由1个桌面，4个桌腿组成．如果1立方米木料可以做方桌的桌面50个或桌腿300条，现有5立方米木料．那么用多少立方米木料做桌面，多少立方米木料做桌腿做出的桌面和桌腿能恰好配成方桌？设生产桌面、桌腿的木料分别是x、y立方米，则符合题意的方程是（ ）
| A． | 50x+300y=1 | B． | 50x+300 y=5 | C． | 50x=1200y | D． | 200x=300y |
10．
如图，已知a∥b，三角形直角顶点在直线a上，已知∠1=25°18′27″，则∠2度数是（ ）
如图，已知a∥b，三角形直角顶点在直线a上，已知∠1=25°18′27″，则∠2度数是（ ）| A． | 25°18′27″ | B． | 64°41′33″ | C． | 74°4133″ | D． | 64°41′43″ |
8．
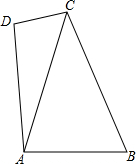如图，在△ABC中，AC=BC=4，将线段AB绕点A逆时针旋转90°，连接CD，则线段CD的最小值是（ ）
如图，在△ABC中，AC=BC=4，将线段AB绕点A逆时针旋转90°，连接CD，则线段CD的最小值是（ ）| A． | $\sqrt{2}$ | B． | 2 | C． | 2$\sqrt{2}$-2 | D． | 4$\sqrt{2}$-4 |