题目内容
14.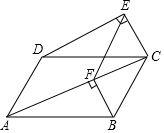 如图,已知四边形ABCD是平行四边形,∠EDC=∠CAB,∠DEC=90°.
如图,已知四边形ABCD是平行四边形,∠EDC=∠CAB,∠DEC=90°.(1)求证:AC∥DE;
(2)过点B作BF⊥AC于点F,连接EF,试判断四边形ADEF的形状,并说明理由.
分析 (1)只要证明∠EDC=∠DCA即可解决问题;
(2)结论:四边形ADEF是平行四边形.只要证明CE∥BF,CE=BF即可;
解答 (1)证明:∵四边形ABCD是平行四边形,
∴AB∥CD,
∴∠DCA=∠CAB,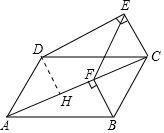
∵∠EDC=∠CAB,
∴∠EDC=∠DCA,
∴DE∥AC.
(2)解:结论:四边形ADEF是平行四边形.
理由:作DH⊥AC于H.
∵AC∥DE,∠DEC=90°,
∴∠DEC=∠ECF=∠DHC=90°,
∴四边形DECH是矩形,
∴DH=EC,
在△ADH和△CBF中,
$\left\{\begin{array}{l}{∠DAH=∠FCB}\\{∠DHA=∠BFC=90°}\\{AD=BC}\end{array}\right.$,
∴△ADH≌△BCF,
∴DH=BF=CE,
∵BF∥CE,
∴四边形EFBC是平行四边形.
点评 本题考查平行四边形的判定和性质、全等三角形的判定和性质等知识,矩形的判定和性质等知识,解题的关键是学会添加常用辅助线,构造全等三角形解决问题,属于中考常考题型.

练习册系列答案
相关题目
19.在二元一次方程:2x-3y=5中,用x表示y正确的是( )
| A. | 2x=5+3y | B. | 3y=5-2x | C. | x=$\frac{3y+5}{2}$ | D. | y=$\frac{2x-5}{3}$ |
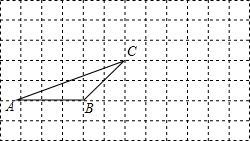 如图,在正方形网格中有一个格点三角形ABC,(即△ABC的各顶点都在格点上),按要求进行下列作图:
如图,在正方形网格中有一个格点三角形ABC,(即△ABC的各顶点都在格点上),按要求进行下列作图: (1)解方程组$\left\{\begin{array}{l}{x+y=2}\\{2x-y=3y-2}\end{array}\right.$;
(1)解方程组$\left\{\begin{array}{l}{x+y=2}\\{2x-y=3y-2}\end{array}\right.$;