题目内容
10.在△ABC中,点G是△ABC的重心,EF过点G,且EF∥BC交AB、AC于点E、F,那么S△AEF:S梯形EBCF的值是4:5.分析 如图,延长AG交BC于H,利用三角形重心的性质得AG=2GH,再根据相似三角形的判定方法得到△AEF∽△ABC,然后利用相似三角形的性质得$\frac{{S}_{△AEF}}{{S}_{△ABC}}$=($\frac{AG}{AH}$)2=$\frac{4}{9}$,则利用比例的性质可得到S△AEF:S梯形EBCF的值.
解答 解:如图,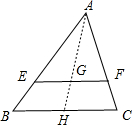 延长AG交BC于H,
延长AG交BC于H,
∵点G是△ABC的重心,
∴AG=2GH,
∵EF∥BC,
∴△AEF∽△ABC,
∴$\frac{{S}_{△AEF}}{{S}_{△ABC}}$=($\frac{AG}{AH}$)2=($\frac{2}{3}$)2=$\frac{4}{9}$,
∴S△AEF:S梯形EBCF=4:5.
故答案为4:5.
点评 本题考查了三角形的重心:三角形的重心是三角形三边中线的交点.重心到顶点的距离与重心到对边中点的距离之比为2:1. 也考查了相似三角形的判定与性质.

练习册系列答案
相关题目
1.一张方桌由1个桌面,4个桌腿组成.如果1立方米木料可以做方桌的桌面50个或桌腿300条,现有5立方米木料.那么用多少立方米木料做桌面,多少立方米木料做桌腿做出的桌面和桌腿能恰好配成方桌?设生产桌面、桌腿的木料分别是x、y立方米,则符合题意的方程是( )
| A. | 50x+300y=1 | B. | 50x+300 y=5 | C. | 50x=1200y | D. | 200x=300y |
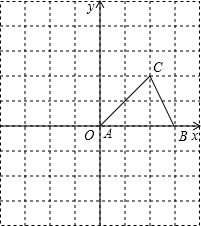 如图,△ABC的顶点A在原点,B、C坐标分别为B(3,0)、C(2,2),将△ABC向左平移2个单位后再向下平移1单位,可得到△A′B′C′.
如图,△ABC的顶点A在原点,B、C坐标分别为B(3,0)、C(2,2),将△ABC向左平移2个单位后再向下平移1单位,可得到△A′B′C′.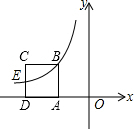 如图,正方形ABCD的边长为2,AD边在x轴负半轴上,反比例函数y=$\frac{k}{x}$(x<0)的图象经过点B和CD边中点E,则k的值为-4.
如图,正方形ABCD的边长为2,AD边在x轴负半轴上,反比例函数y=$\frac{k}{x}$(x<0)的图象经过点B和CD边中点E,则k的值为-4.