题目内容
1. 如图,A,B,C,D是⊙O的四等分点,点P是劣弧$\widehat{AB}$上的动点,当点P从点A向点B运动时(点P不与A、B重合).若⊙O的半径为2.则图中阴影部分面积的最大值是( )
如图,A,B,C,D是⊙O的四等分点,点P是劣弧$\widehat{AB}$上的动点,当点P从点A向点B运动时(点P不与A、B重合).若⊙O的半径为2.则图中阴影部分面积的最大值是( )| A. | $\sqrt{2}$ | B. | 2 | C. | 2$\sqrt{2}$ | D. | 2$\sqrt{2}$+2 |
分析 因为S阴=S△PDC-S△OCD,所以△PDC面积最大时,阴影部分的面积最大,推出当P′是$\widehat{AB}$的中点时,△P′DC的面积最大,由此即可解决问题.
解答 解:如图,∵A,B,C,D是⊙O的四等分点,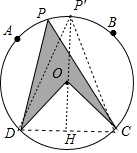
∴∠DOC=90°,
∴DC=2$\sqrt{2}$,
∵S阴=S△PDC-S△OCD,
∴△PDC面积最大时,阴影部分的面积最大,
∴当P′是$\widehat{AB}$的中点时,
△P′DC的面积最大,
易知此时S△P′DC=$\frac{1}{2}$$•2\sqrt{2}$•(2+$\sqrt{2}$)=2$\sqrt{2}$+2,S△ODC=$\frac{1}{2}$×2×2=2,
∴阴影部分的面积的最大值=2$\sqrt{2}$+2-2=2$\sqrt{2}$,
故选C.
点评 本题考查圆的有关知识,三角形的面积等知识,解题的关键是学会用转化的思想思考问题,属于中考选择题中的压轴题.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
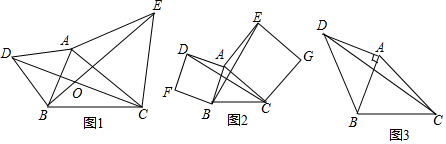
10. 如图,已知a∥b,三角形直角顶点在直线a上,已知∠1=25°18′27″,则∠2度数是( )
如图,已知a∥b,三角形直角顶点在直线a上,已知∠1=25°18′27″,则∠2度数是( )
 如图,已知a∥b,三角形直角顶点在直线a上,已知∠1=25°18′27″,则∠2度数是( )
如图,已知a∥b,三角形直角顶点在直线a上,已知∠1=25°18′27″,则∠2度数是( )| A. | 25°18′27″ | B. | 64°41′33″ | C. | 74°4133″ | D. | 64°41′43″ |
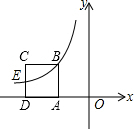 如图,正方形ABCD的边长为2,AD边在x轴负半轴上,反比例函数y=$\frac{k}{x}$(x<0)的图象经过点B和CD边中点E,则k的值为-4.
如图,正方形ABCD的边长为2,AD边在x轴负半轴上,反比例函数y=$\frac{k}{x}$(x<0)的图象经过点B和CD边中点E,则k的值为-4.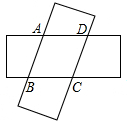 如图用两个完全相同的1cm×4cm长方形纸片,其中心用细铁丝串起来,使纸片交叉叠合,旋转纸片,保持重叠部分形状为菱形,则菱形的最大面积是$\frac{17}{8}$cm2.
如图用两个完全相同的1cm×4cm长方形纸片,其中心用细铁丝串起来,使纸片交叉叠合,旋转纸片,保持重叠部分形状为菱形,则菱形的最大面积是$\frac{17}{8}$cm2.