题目内容
12.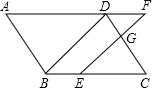 如图,在平行四边形ABCD中,点E在边BC上,点F在边AD的延长线上,且DF=BE,EF与CD交于点G.
如图,在平行四边形ABCD中,点E在边BC上,点F在边AD的延长线上,且DF=BE,EF与CD交于点G.(1)求证:BD∥EF;
(2)若点G是DC的中点,BE=6,求边AD的长.
分析 (1)根据平行四边的判定与性质,可得答案;
(2)根据ASA证明△DGF≌△CGE,再根据全等三角形的性质与平行四边形的性质即可求解.
解答 解:(1)证明:∵四边形ABCD是平行四边形,
∴AD∥BC,
∵DF=BE,
∴四边形DBEF是平行四边形,
∴BD∥EF;
(2)解:∵AD∥BC,
∴∠FDG=∠C,
∵点G是DC的中点,
∴DG=CG,
在△DGF与△CGE中,
$\left\{\begin{array}{l}{∠FDG=∠C}\\{DG=CG}\\{∠DGF=∠CGE}\end{array}\right.$,
∴△DGF≌△CGE,
∴DF=CE,
∵DF=BE=6,
∴EC=DF=6,
∴BC=BE+EC=12,
∵四边形ABCD是平行四边形,
∴AD=BC=12.
点评 本题考查了平行四边形的判定与性质,全等三角形的判定与性质,关键是证明△DGF≌△CGE.

练习册系列答案
相关题目
1.一张方桌由1个桌面,4个桌腿组成.如果1立方米木料可以做方桌的桌面50个或桌腿300条,现有5立方米木料.那么用多少立方米木料做桌面,多少立方米木料做桌腿做出的桌面和桌腿能恰好配成方桌?设生产桌面、桌腿的木料分别是x、y立方米,则符合题意的方程是( )
| A. | 50x+300y=1 | B. | 50x+300 y=5 | C. | 50x=1200y | D. | 200x=300y |
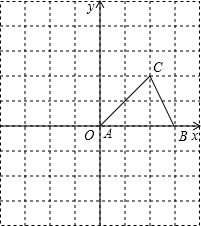 如图,△ABC的顶点A在原点,B、C坐标分别为B(3,0)、C(2,2),将△ABC向左平移2个单位后再向下平移1单位,可得到△A′B′C′.
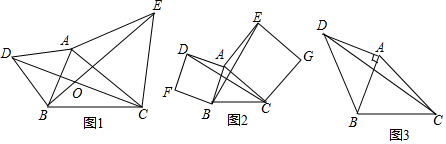
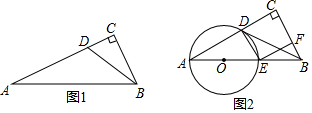
如图,△ABC的顶点A在原点,B、C坐标分别为B(3,0)、C(2,2),将△ABC向左平移2个单位后再向下平移1单位,可得到△A′B′C′.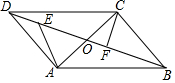 如图,点O为?ABCD的对角线AC,BD的交点,∠BCO=90°,∠BOC=60°,BD=8,点E是OD上的一动点,点F是OB上的一动点(E,F不与端点重合),且DE=OF,连接AE,CF.
如图,点O为?ABCD的对角线AC,BD的交点,∠BCO=90°,∠BOC=60°,BD=8,点E是OD上的一动点,点F是OB上的一动点(E,F不与端点重合),且DE=OF,连接AE,CF.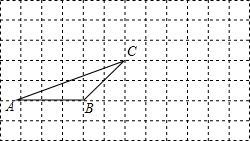 如图,在正方形网格中有一个格点三角形ABC,(即△ABC的各顶点都在格点上),按要求进行下列作图:
如图,在正方形网格中有一个格点三角形ABC,(即△ABC的各顶点都在格点上),按要求进行下列作图: