题目内容
17．已知等边△ABC的高为4，在这个三角形所在的平面内有一点P，若点P到AB的距离是1，点P到AC的距离是2，则所有符合条件的点P到直线的距离之和是12．分析 根据题意得出点在与AB平行且与AB的距离为1的两条直线上，同时点P在与AC平行且与AC的距离为2的直线上，得出点P的个数，即可得出结果．
解答 解：到AB的距离是1的点P在与AB平行且与AB的距离为1的两条直线a、b上，
到AC的距离是2的点P在与AC平行且与AC的距离为2的直线c、d上，
直线a、b、c、d的交点即为满足条件的点P，这样的点有4个，如图所示：
∴所有符合条件的点P到直线的距离之和=4（1+2）=12；
故答案为：12．
点评 本题考查了等边三角形的性质、点到直线的距离；熟练掌握等边三角形的性质，通过作图得出点P的个数是解决问题的关键．
练习册系列答案
相关题目
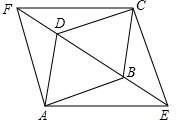如图，在菱形ABCD中，AB=2，∠BAD=60°，将对角线BD向两个相反的方向延长，分别至点E与点F，且BE=DF．
如图，△ABF≌△CDE，A与C，B与D分别是对应顶点，∠B=35°，∠BAE=45°，求∠EFC的度数．