题目内容
5.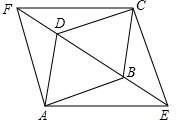 如图,在菱形ABCD中,AB=2,∠BAD=60°,将对角线BD向两个相反的方向延长,分别至点E与点F,且BE=DF.
如图,在菱形ABCD中,AB=2,∠BAD=60°,将对角线BD向两个相反的方向延长,分别至点E与点F,且BE=DF.(1)求证:四边形AECF是菱形.
(2)若∠AEC是锐角,求BE的长的取值范围S.
分析 (1)连接AC交BD于O,由菱形的性质得出OA=OC,OB=OD,AC⊥BD,证出OE=OF,得出四边形AECF是平行四边形,由AC⊥BD,即可得出四边形AECF是菱形.
(2)先证明△ABD是等边三角形,得出BD=AB=2,得出OB=$\frac{1}{2}$BD=1,由勾股定理求出OA,得出AC,当∠AEC=90°时,△ACE是等腰直角三角形,得出BE=$\sqrt{3}$-1,若∠AEC是锐角,即可得出BE的长的取值范围.
解答 (1)证明:连接AC交BD于O,如图所示: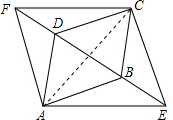 ∵四边形ABCD是菱形,
∵四边形ABCD是菱形,
∴AB=BC=CD=DA,OA=OC,OB=OD,AC⊥BD,
∵BE=DF,
∴OE=OF,
∴四边形AECF是平行四边形,
又∵AC⊥BD,
∴四边形AECF是菱形.
(2)解:∵∠BAD=60°,
∴△ABD是等边三角形,
∴BD=AB=2,
∴OB=$\frac{1}{2}$BD=1,
∴OA=$\sqrt{{2}^{2}-{1}^{2}}$=$\sqrt{3}$,
∴AC=2$\sqrt{3}$,
当∠AEC=90°时,△ACE是等腰直角三角形,
∵AC⊥BD,
∴OE=$\frac{1}{2}$AC=$\sqrt{3}$,
∴BE=$\sqrt{3}$-1,
∴若∠AEC是锐角,BE的长的取值范围S>$\sqrt{3}$-1.
点评 本题考查了菱形的判定与性质、平行四边形的判定、勾股定理、等边三角形的判定与性质、等腰直角三角形的判定与性质;熟练掌握菱形的判定与性质,并能进行推理论证与计算是解决问题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
11.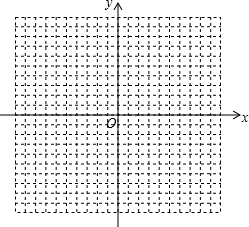 在同一坐标系中画出下列函数的图象:
在同一坐标系中画出下列函数的图象:
(1)y=-x2;
(2)y=-(x+2)2
(3)y=-(x-1)2
 在同一坐标系中画出下列函数的图象:
在同一坐标系中画出下列函数的图象:(1)y=-x2;
(2)y=-(x+2)2
(3)y=-(x-1)2
| x | … | -4 | -3 | -2 | -1 | 0 | 1 | 2 | 3 | 4 | … |
| y=-x2 | … | … | |||||||||
| y=-(x+2)2 | … | … | |||||||||
| y=-(x-1)2 | … | … |
 点P在点O正西方300m处,点Q在点O正北方150m处,甲从点P出发,向正东走;乙从点Q出发,向正北走,两人同时出发,速度相同.
点P在点O正西方300m处,点Q在点O正北方150m处,甲从点P出发,向正东走;乙从点Q出发,向正北走,两人同时出发,速度相同. 如图,已知∠1=65°,∠2=115°.直线BC与DF平行吗?为什么?
如图,已知∠1=65°,∠2=115°.直线BC与DF平行吗?为什么?