题目内容
2．
如图，△ABF≌△CDE，A与C，B与D分别是对应顶点，∠B=35°，∠BAE=45°，求∠EFC的度数．
分析 由已知全等三角形的对应角相等推知∠B=∠D=35°∠DCF=∠BAE=45°；然后由三角形外角定理来求∠EFC的度数．
解答 解：∵△ABF≌△CDE，∠B=35°，∠BAE=45°，
∴∠B=∠D=35°，∠DCF=∠BAE=45°，
∴∠EFC=∠D+∠DCF=80°．
即∠EFC的度数是80°．
点评 本题考查了全等三角形的性质．
性质1：全等三角形的对应边相等．
性质2：全等三角形的对应角相等．
练习册系列答案
相关题目
10．下列说法错误的是（ ）
| A． | 圆周率π是无限不循环小数，它不是有理数 | |
| B． | 负整数与负分数统称为负有理数 | |
| C． | 正有理数与负有理数组成全体有理数 | |
| D． | $\frac{20}{5}$不是分数，而是整数 |
11．
在同一坐标系中画出下列函数的图象：
（1）y=-x2；
（2）y=-（x+2）2
（3）y=-（x-1）2
在同一坐标系中画出下列函数的图象：（1）y=-x2；
（2）y=-（x+2）2
（3）y=-（x-1）2
| x | … | -4 | -3 | -2 | -1 | 0 | 1 | 2 | 3 | 4 | … |
| y=-x2 | … | … | |||||||||
| y=-（x+2）2 | … | … | |||||||||
| y=-（x-1）2 | … | … |
如图，已知∠1=65°，∠2=115°．直线BC与DF平行吗？为什么？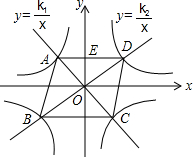
如图，经过O的直线AC，BD分别与反比例函数y=$\frac{{k}_{1}}{x}$（k1＜0），y=$\frac{{k}_{2}}{x}$（k＞0）相交于点A，C，B，D，且AC⊥BD