题目内容
5.已知x=$\frac{\sqrt{7}+\sqrt{3}}{2}$,y=$\frac{\sqrt{7}-\sqrt{3}}{2}$,求下列各式的值.(1)x2+xy+y2;
(2)$\frac{y}{x}+\frac{x}{y}$.
分析 由x=$\frac{\sqrt{7}+\sqrt{3}}{2}$,y=$\frac{\sqrt{7}-\sqrt{3}}{2}$,得出x+y=$\sqrt{7}$,xy=1;
(1)原式=(x+y)2-xy;
(2)原式=$\frac{(x+y)^{2}-2xy}{xy}$;
整体代入求得答案即可.
解答 解:∵x=$\frac{\sqrt{7}+\sqrt{3}}{2}$,y=$\frac{\sqrt{7}-\sqrt{3}}{2}$,
∴x+y=$\sqrt{7}$,xy=1;
(1)原式=(x+y)2-xy=7-1=6;
(2)原式=$\frac{(x+y)^{2}-2xy}{xy}$=5.
点评 此题考查二次根式的化简求值,利用因式分解先把式子变形,再整体代入是解决问题的关键.

练习册系列答案
 轻松课堂单元期中期末专题冲刺100分系列答案
轻松课堂单元期中期末专题冲刺100分系列答案
相关题目
15.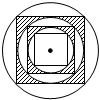 如图,在半径为1的圆内作一个内接正方形,然后作这个正方形的内切圆,又在这个内切圆中作内接正方形,依此类推,第6个内切圆的面积是( )
如图,在半径为1的圆内作一个内接正方形,然后作这个正方形的内切圆,又在这个内切圆中作内接正方形,依此类推,第6个内切圆的面积是( )
 如图,在半径为1的圆内作一个内接正方形,然后作这个正方形的内切圆,又在这个内切圆中作内接正方形,依此类推,第6个内切圆的面积是( )
如图,在半径为1的圆内作一个内接正方形,然后作这个正方形的内切圆,又在这个内切圆中作内接正方形,依此类推,第6个内切圆的面积是( )| A. | $\frac{π}{16}$ | B. | $\frac{π}{32}$ | C. | $\frac{π}{64}$ | D. | $\frac{π}{128}$ |
10.下列说法错误的是( )
| A. | 圆周率π是无限不循环小数,它不是有理数 | |
| B. | 负整数与负分数统称为负有理数 | |
| C. | 正有理数与负有理数组成全体有理数 | |
| D. | $\frac{20}{5}$不是分数,而是整数 |
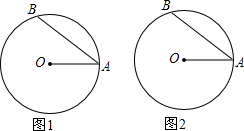 如图,⊙O的半径OA=5cm,AB是弦,∠OAB=30°,现有一动点C从A出发,沿弦AB运动到B,再从B沿劣弧BA回到点A.
如图,⊙O的半径OA=5cm,AB是弦,∠OAB=30°,现有一动点C从A出发,沿弦AB运动到B,再从B沿劣弧BA回到点A. 点P在点O正西方300m处,点Q在点O正北方150m处,甲从点P出发,向正东走;乙从点Q出发,向正北走,两人同时出发,速度相同.
点P在点O正西方300m处,点Q在点O正北方150m处,甲从点P出发,向正东走;乙从点Q出发,向正北走,两人同时出发,速度相同.