题目内容
9.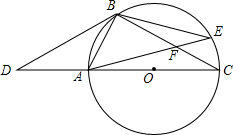 如图,点D是⊙O的直径CA延长线上的一点,点B在⊙O上,且AB=AD=AO.
如图,点D是⊙O的直径CA延长线上的一点,点B在⊙O上,且AB=AD=AO.(1)求证:BD是⊙O的切线;
(2)当点E在⊙O上的什么位置时,BE=AD,并说明理由.
分析 (1)连接OB,如图,易证△OAB是等边三角形,则有∠BAO=∠BOA=∠ABO=60°,要证BD是⊙O的切线,只需证∠DBO=90°,只需证∠ABD=30°即可;
(2)当点E在$\widehat{BC}$的中点时,易证∠BAE=∠BEA=30°,即可得到BE=AB,再结合条件AB=AD就可解决问题.
解答 解:(1)连接OB,如图,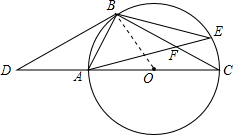
∵AB=AO=OB,
∴△OAB是等边三角形,
∴∠BAO=∠BOA=∠ABO=60°.
∵AB=AD,
∴∠D=∠ABD,
∴∠BAO=2∠D=2∠ABD=60°,
∴∠D=∠ABD=30°,
∴∠DBO=90°,
∴BD是⊙O的切线;
(2)当点E在$\widehat{BC}$的中点时,BE=AD.
理由如下:
∵点E是$\widehat{BC}$的中点,
∴∠BAE=∠EAC=$\frac{1}{2}$∠BAC=30°.
∵∠BEA=$\frac{1}{2}$∠AOB=30°,
∴∠BAE=∠BEA,
∴BE=AB.
∵AB=AD,
∴BE=AD.
点评 本题主要考查了等边三角形的判定与性质、切线的判定、等腰三角形的性质、圆周角定理、圆弧与圆周角的关系等知识,要证直线与圆相切,若已知直线与圆的交点,只需证过该点的半径与直线垂直;若未知直线与圆的交点,只需证圆心到直线的距离等于半径.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
1.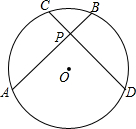 如图1,在⊙O中,弦AB与CD交于点P,若AB=CD,则$\widehat{AC}$与$\widehat{BD}$的大小关系是( )
如图1,在⊙O中,弦AB与CD交于点P,若AB=CD,则$\widehat{AC}$与$\widehat{BD}$的大小关系是( )
 如图1,在⊙O中,弦AB与CD交于点P,若AB=CD,则$\widehat{AC}$与$\widehat{BD}$的大小关系是( )
如图1,在⊙O中,弦AB与CD交于点P,若AB=CD,则$\widehat{AC}$与$\widehat{BD}$的大小关系是( )| A. | $\widehat{AC}$=$\widehat{BD}$ | B. | $\widehat{AC}$$>\widehat{BD}$ | C. | $\widehat{AC}$$<\widehat{BD}$ | D. | 不能确定 |
18.下列说法正确的是( )
| A. | 一个数的平方根一定是两个 | |
| B. | 一个正数的平方根一定是它的算术平方根 | |
| C. | 一个正数的算术平方根一定大于这个数的相反数 | |
| D. | 一个数的正的平方根是算术平方根 |
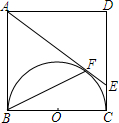 如图,正方形ABCD的边长为4cm,以正方形的边BC为直径在正方形内作半圆,再经过A点作半圆的切线AE,与半圆相切于F点,与DC相交于E点,求:
如图,正方形ABCD的边长为4cm,以正方形的边BC为直径在正方形内作半圆,再经过A点作半圆的切线AE,与半圆相切于F点,与DC相交于E点,求: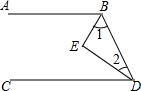 如图,BE、DE分别平分∠ABD和∠CDB,∠1+∠2=90°,问AB与CD平行吗?说明理由.
如图,BE、DE分别平分∠ABD和∠CDB,∠1+∠2=90°,问AB与CD平行吗?说明理由.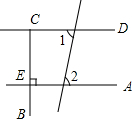 如图,根据图形填空,其中横线上填上结论,括号中填推理理由.
如图,根据图形填空,其中横线上填上结论,括号中填推理理由.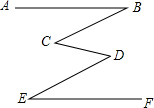 如图,已知AB∥EF,∠ABC=∠DEF,试判断BC和DE的位置关系,并说明理由.
如图,已知AB∥EF,∠ABC=∠DEF,试判断BC和DE的位置关系,并说明理由.