题目内容

10．已知圆内接正六边形与正方形面积之差为11cm2，求该圆内接正三角形的面积．

分析 根据圆内接正六边形与正方形面积与半径的关系进行解答即可．

解答 解：设圆半径为r，则圆内接正六边形的面积为$\frac{3\sqrt{3}}{2}{r}^{2}$，圆内接正方形的面积为2r2，
因为圆内接正六边形与正方形面积之差为11cm2，
可得：$\frac{3\sqrt{3}}{2}{r}^{2}-2{r}^{2}=11$，
解得：r2=$6\sqrt{3}+4$，
所以圆内接正三角形的面积=$\frac{3\sqrt{3}}{2}×（6\sqrt{3}+4）=27+6\sqrt{3}$．

点评 本题考查的正多边形和圆问题；理解圆内接正六边形与正方形面积与半径的关系是解答此题的关键．

练习册系列答案
相关题目
14．一个不透明的袋子里装有8个球，其中有2个红球，6个白球，这些球除颜色外其它均相同，现从中随机摸出一个球，则摸出的球是红球的概率为$\frac{1}{4}$．
1．已知等边△ABC和Rt△DEF按如图1所示的位置放置，点B、D重合，且点E、B（D）、C在同一条直线上．其中∠DEF=90°，∠EDF=30°，AB=DE=$6\sqrt{3}$，现将△DEF沿直线BC以每秒$\sqrt{3}$个单位向右平移，直至E点与C点重合时停止运动，设运动时间为t秒．

（1）试求出在平移过程中，点F落在△ABC的边上时的t值；
（2）试求出在平移过程中△ABC和Rt△DEF重叠部分的面积S与t的函数关系式；
（3）当D与C重合时（如图2），DF与AB交于G点，点H为直线DF上一动点，现将△BDH绕点D顺时针旋转60°得到△ACK，是否存在点H，使得△ACK为等腰三角形？若存在，连接AF，并求出△AFK的面积；若不存在，请说明理由．
18．如图1，矩形ABCD，AD＞AB＞$\frac{1}{2}$AC，P和Q两点分别从点A出发，点P沿着A-C-D的折线段以每秒2各单位长度运动，同时点Q沿着AD线段以每秒1各单位长度运动，AP的中垂线交AD于点M，设QM的长为y，运动时间为x，y与x的关系如图2所示：．
（1）AB=3，AD=4；
（2）求y与x的函数关系式，并写出x的取值范围；
（3）求x为何值时，DQ=DP？
5．计算题：
（1）（$\sqrt{18}$-2$\sqrt{2}$）$\sqrt{\frac{1}{12}}$；
（2）（$\sqrt{2}$-$\sqrt{12}$）（$\sqrt{18}$+$\sqrt{48}$）；
（3）（5$\sqrt{\frac{1}{2}}$-6$\sqrt{\frac{3}{2}}$）（$\frac{1}{4}\sqrt{8}$-$\sqrt{\frac{2}{3}}$）；
（4）（$\frac{1}{2}\sqrt{3}$+$\sqrt{8}$）（$\sqrt{8}$-$\frac{1}{2}\sqrt{3}$）；
（5）（10$\sqrt{48}$-6$\sqrt{27}$+4$\sqrt{12}$）$÷\sqrt{6}$．
（6）（$\sqrt{12}$-2$\sqrt{18}$）2．
15．抛物线y=3（x+1）2的对称轴是x=-1，顶点坐标是（-1，0）．
2．计算：$\frac{\sqrt{20}+\sqrt{5}}{\sqrt{5}}$-$\sqrt{12}$÷$\sqrt{\frac{1}{3}}$．
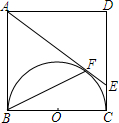19．如图，正方形ABCD的边长为4cm，以正方形的边BC为直径在正方形内作半圆，再经过A点作半圆的切线AE，与半圆相切于F点，与DC相交于E点，求：
（1）△ADE的面积；
（2）求线段BF的长．
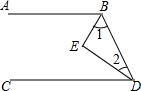20．如图，BE、DE分别平分∠ABD和∠CDB，∠1+∠2=90°，问AB与CD平行吗？说明理由．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网