题目内容
14.计算:(1)$\sqrt{\frac{2b}{a}}$•$\sqrt{\frac{a}{18b}}$=$\frac{1}{3}$;
(2)$\sqrt{2{5}^{2}-2{4}^{2}}$=7;
(2)3$\sqrt{5a}$•2$\sqrt{10b}$=30$\sqrt{2ab}$;
(4)$\sqrt{\frac{16{b}^{2}c}{{a}^{2}}}$=|$\frac{4b\sqrt{c}}{a}$|.
分析 (1)直接利用二次根式的性质化简求出答案;
(2)直接利用二次根式的性质化简求出答案;
(3)直接利用二次根式的性质化简求出答案;
(4)直接利用二次根式的性质化简求出答案.
解答 解:(1)$\sqrt{\frac{2b}{a}}$•$\sqrt{\frac{a}{18b}}$=$\sqrt{\frac{2ab}{18ab}}$=$\frac{1}{3}$.
故答案为:$\frac{1}{3}$;
(2)$\sqrt{2{5}^{2}-2{4}^{2}}$=$\sqrt{625-576}$=$\sqrt{49}$=7.
故答案为:7;
(2)3$\sqrt{5a}$•2$\sqrt{10b}$=6$\sqrt{50ab}$=30$\sqrt{2ab}$.
故答案为:30$\sqrt{2ab}$;
(4)$\sqrt{\frac{16{b}^{2}c}{{a}^{2}}}$=|$\frac{4b\sqrt{c}}{a}$|.
故答案为:|$\frac{4b\sqrt{c}}{a}$|.
点评 此题主要考查了二次根式乘除运算,正确化简二次根式是解题关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
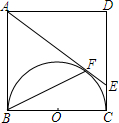 如图,正方形ABCD的边长为4cm,以正方形的边BC为直径在正方形内作半圆,再经过A点作半圆的切线AE,与半圆相切于F点,与DC相交于E点,求:
如图,正方形ABCD的边长为4cm,以正方形的边BC为直径在正方形内作半圆,再经过A点作半圆的切线AE,与半圆相切于F点,与DC相交于E点,求:
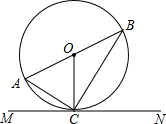 直线MN切⊙O于点C,AB是⊙O的直径且∠CAB=53°,则∠BOC=106°,∠ACB=90°,∠ACM=37°,∠BCN=53°.
直线MN切⊙O于点C,AB是⊙O的直径且∠CAB=53°,则∠BOC=106°,∠ACB=90°,∠ACM=37°,∠BCN=53°.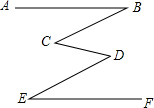 如图,已知AB∥EF,∠ABC=∠DEF,试判断BC和DE的位置关系,并说明理由.
如图,已知AB∥EF,∠ABC=∠DEF,试判断BC和DE的位置关系,并说明理由.