题目内容
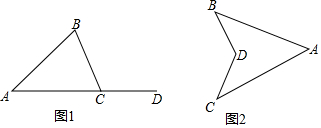
19.如图1,∠BCD是△ABC外角,则有∠BCD=∠A+∠B,由于∠A,∠B都是正数,所以有∠BCD>∠A,∠BCD>∠B,即“三角形的一个外角大于任何和它不相邻的一个内角”.利用上述结论尝试证明;如图2,求证:(1)∠BDC>∠A,(2)∠BDC=∠B+∠C+∠A.
分析 (1)根据“三角形的一个外角大于任何一个和它不相邻的内角”来比较大小.
(2)根据“三角形的外角等于与它不相邻的两个内角和”来求∠BDC=∠B+∠C+∠A
解答  证明:(1)延长BD交AC于E,则∠BDC>∠DEC,而∠DEC>∠A,所以∠BDC>∠A;
证明:(1)延长BD交AC于E,则∠BDC>∠DEC,而∠DEC>∠A,所以∠BDC>∠A;
(2)由∠BDC=∠C+∠DEC,而∠DEC=∠A+∠B,所以∠BDC=∠A+∠B+∠C.
点评 主要考查了三角形的内角和外角之间的关系:
(1)三角形的外角等于与它不相邻的两个内角和;
(2)三角形的一个外角大于任何一个和它不相邻的内角.

练习册系列答案
相关题目
19.若不等式ax<5的解集是x>-1,则a的值为( )
| A. | -15 | B. | -5 | C. | -6 | D. | -9 |
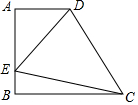 如图,在直角梯形ABCD中,AD∥BC(BC>AD),∠B=90°,AB=BC=12,E是AB上一点,且∠DCE=45°,BE=4,求DE的长.
如图,在直角梯形ABCD中,AD∥BC(BC>AD),∠B=90°,AB=BC=12,E是AB上一点,且∠DCE=45°,BE=4,求DE的长.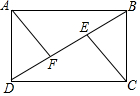 如图,在四边形ABCD中,E,F是对角线BD上两点,其中AD∥BC,∠DAF=∠BCE,AD=BC.求证:AB∥CD.
如图,在四边形ABCD中,E,F是对角线BD上两点,其中AD∥BC,∠DAF=∠BCE,AD=BC.求证:AB∥CD.