题目内容
20.某商店如果将进货价为8元的商品按每件10元售出,每天可销售200件,现在采用提高售价,减少进货量的方法增加利润,已知这种商品每涨价1元,其销量就减少20件.( 1)要使每天获得利润700元,请你帮忙确定售价;
( 2)问售价定在多少时能使每天获得的利润最多?并求出最大利润.
分析 (1)设售价为x元,总利润为W元,则销售量为[200-20(x-10)]件,根据利润=数量×每件的利润,求出W与x之间的函数关系式,再将W=700代入解析式就可以求出售价;
(2)将函数关系式化为顶点式就可以求出结论.
解答 解:(1)设售价为x元,总利润为W元,则销售量为[200-20(x-10)]件,由题意,得
W=(x-8)[200-20(x-10)],
W=-20x2+560x-3200,
当W=700时,700=-20x2+560x-3200,
解得:x1=13,x2=15.
答:要使每天获得的利润为700元,则售价为13元或15元;
(2)∵W=-20x2+560x-3200,
∴W=-20(x-14)2+720.
∴a=-20<0,
∴W有最大值,
∴x=14时,W最大=720.
答:当售价定为14元时,才能使所赚利润最大,最大利润为720.
点评 本题考查了销售问题的数量关系的运用,二次函数的性质的运用,抛物线的顶点式的运用,解答时根据利润=数量×每件的利润,求出W与x之间的函数关系式是关键.

练习册系列答案
 快捷英语周周练系列答案
快捷英语周周练系列答案
相关题目
10.如图,已知△ABC的六个元素,那么甲、乙、丙三个三角形中和△ABC全等的三角形是( )


| A. | 甲和乙 | B. | 甲和丙 | C. | 只有甲 | D. | 只有丙 |
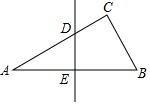 如图,△ABC中,∠C=90°,∠A=30°,AB的垂直平分线交AC于D,交AB于E,CD=1,则AC=3.
如图,△ABC中,∠C=90°,∠A=30°,AB的垂直平分线交AC于D,交AB于E,CD=1,则AC=3.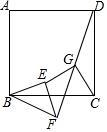 已知:正方形ABCD和RT△BEF,BE=EF,G是DF中点,判断EG和CG的关系并说明理由.
已知:正方形ABCD和RT△BEF,BE=EF,G是DF中点,判断EG和CG的关系并说明理由.