题目内容
4.某社区计划对面积为1800m2的区域进行绿化,经投标,由甲、乙两个工程队来完成,已知甲队每天能绿化的面积是乙队每天能绿化面积的2倍,并且在独立完成400m2的绿化时,甲队比乙队少用4天.(1)求甲、乙两队每天各能完成的绿化面积;
(2)若甲队每天的施工费用是0.6万元,乙队每年的施工费用是0.25万元,且甲、乙两队施工的总天数不超过26天,则怎样安排甲、乙两队的施工天数,使施工费用最低?并求出最低费用.
分析 (1)根据题意可以列出相应的分式方程,从而可以解答本题,注意分式方程要检验;
(2)根据题意可以得到费用与甲队的函数关系,再根据甲、乙两队施工的总天数不超过26天可以得到相应的不等式,然后根据一次函数的性质即可解答本题.
解答 (1)解:设乙队每天能绿化的面积是xm2,则甲队每天能绿化的面积是2xm2.
$\frac{400}{x}-\frac{400}{2x}=4$,
解得,x=50,
经检验,x=50是原方程的解,
∴2x=100,
答:甲队每天能绿化的面积是100m2,乙队每天能绿化的面积是50m2;
(2)设:甲队施工m天,总费用为W万元.
W=0.6m+$\frac{1800-100m}{50}×0.25$,
化简,得
W=0.1m+9,
∵m+$\frac{1800-100m}{50}$≤26,
解得,m≥10,
∴当m=10时,W取得最小值,此时W=0.1×10+9=10,$\frac{1800-100m}{50}$=16,
答:安排甲队施工10天、乙队的施工16天时,使施工费用最低,最低费用是10万元.
点评 本题考查一次函数的应用、分式方程的应用,解答本题的关键是明确题意,找出所求问题需要的条件,利用方程的思想和一次函数的性质解答.

练习册系列答案
 暑假作业海燕出版社系列答案
暑假作业海燕出版社系列答案 本土教辅赢在暑假高效假期总复习云南科技出版社系列答案
本土教辅赢在暑假高效假期总复习云南科技出版社系列答案 暑假作业北京艺术与科学电子出版社系列答案
暑假作业北京艺术与科学电子出版社系列答案 第三学期赢在暑假系列答案
第三学期赢在暑假系列答案
相关题目
13.计算$\sqrt{27}$-$\sqrt{3}$的结果是( )
| A. | 24 | B. | $\sqrt{24}$ | C. | 2$\sqrt{3}$ | D. | 3$\sqrt{2}$ |
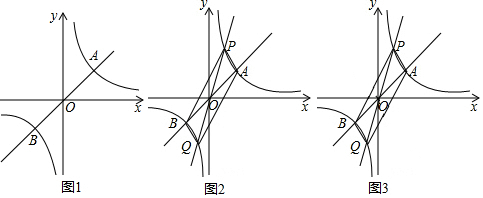
 如图,AB∥CD,AE、DF分别是∠BAD、∠CDA的角平分线,那么AE与DF是否平行?请说明理由.
如图,AB∥CD,AE、DF分别是∠BAD、∠CDA的角平分线,那么AE与DF是否平行?请说明理由.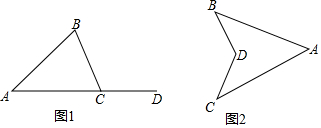
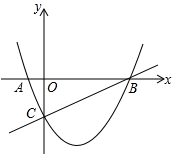 如图,已知抛物线y=ax2-x+c与x轴相交于A、B两点,并与直线y=$\frac{1}{2}$x-2交于B、C两点,其中点C是直线y=x-2与y轴的交点.求抛物线的解析式.
如图,已知抛物线y=ax2-x+c与x轴相交于A、B两点,并与直线y=$\frac{1}{2}$x-2交于B、C两点,其中点C是直线y=x-2与y轴的交点.求抛物线的解析式.