题目内容
14.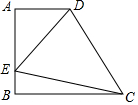 如图,在直角梯形ABCD中,AD∥BC(BC>AD),∠B=90°,AB=BC=12,E是AB上一点,且∠DCE=45°,BE=4,求DE的长.
如图,在直角梯形ABCD中,AD∥BC(BC>AD),∠B=90°,AB=BC=12,E是AB上一点,且∠DCE=45°,BE=4,求DE的长.
分析 过C作CG⊥AD,交AD延长线于G,先证四边形ABCG是正方形(有一组邻边相等的矩形是正方形).
再设DE=x,在Rt△AED中利用勾股定理可求出DE.
解答 解: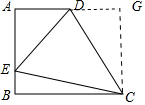
过C作CG⊥AD于G,
在直角梯形ABCD中∵AD∥BC,∠A=∠B=90°,∠CGA=90°,AB=BC,
∴四边形ABCG为正方形,
∴AG=BC=12,
∵∠DCE=45°,由①②可得ED=BE+DG,
设DE=x,则DG=x-4,
∴AD=16-x
在Rt△AED中,∵DE2=AD2+AE2,
∴x2=(16-x)2+82
∴x=10,
即DE=10.
点评 本题考查的是全等三角形的判定和性质、勾股定理的应用,掌握三角形全等的判定定理和性质定理是解题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
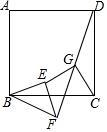 已知:正方形ABCD和RT△BEF,BE=EF,G是DF中点,判断EG和CG的关系并说明理由.
已知:正方形ABCD和RT△BEF,BE=EF,G是DF中点,判断EG和CG的关系并说明理由.
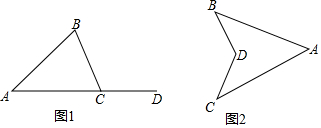
 已知:如图,等边△ABC中,D为BC上一点.CE为△ABC的外角角平分线,连接DE,若DE=DA,求证:△ADE为等边三角形.
已知:如图,等边△ABC中,D为BC上一点.CE为△ABC的外角角平分线,连接DE,若DE=DA,求证:△ADE为等边三角形.