��Ŀ����
4��С����������һ�����⣺��ͼ1����Rt��ABC�У�AC=BC��CD��AB������Ϊ��D��AE��GC��BF��GC������ΪF��E������DE��С��ͨ��̽�����֣���ͼ2������DF��֤����ADE�ա�CDF��ʹ����õ������
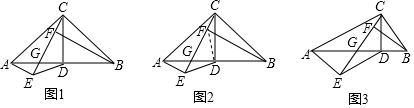
�ο�С��˼������ķ���������������⣺
��1�������Ķ����Ͻ��AE��CF��������ϵ��DE��EF��������ϵ��
��2����ͼ3�������������������AC=BC����Ϊ��AC=kBC����kΪ������k��0���������������䣬��$\frac{EF}{DE}$��ֵ�����ú�k��ʽ�ӱ�ʾ��
���� ��1����ͼ1�У����ۣ�AE=CF��ֻҪ֤����ACE�ա�CBF���ɣ����ۣ�EF=$\sqrt{2}$DE���ɡ�DCF�ա�DAE���Ƴ�DE=DF����CDF=��ADE���Ƴ���EDF=��ADC=90�㣬
�Ƴ���EDF�ǵ���ֱ�������Σ����ɽ�����⣮
��2����ͼ3�У����ۣ�$\frac{EF}{DE}$=$\frac{\sqrt{1+{k}^{2}}}{k}$����취֤����ADE�ס�CDF���Ƴ�$\frac{DE}{DF}$=$\frac{AE}{CF}$=k����ADE=��CDF����EDF=��ADC=90�㣬��DF=m����DE=km��EF=$\sqrt{D{E}^{2}+D{F}^{2}}$=$\sqrt{1+{k}^{2}}$•m���ɴ˼��ɽ�����⣮
��� �⣺��1����ͼ1�У����ۣ�AE=CF���������£�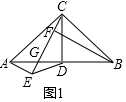
��AC=BC����ACB=��BFC=��AEC=90�㣬
���ACE+��BCF=90�㣬��BCF+��CBF=90�㣬
���ACE=��CBF��
�ڡ�ACE�͡�CBF�У�
$\left\{\begin{array}{l}{��ACE=��CBF}\\{��AEC=��BFC}\\{AC=BC}\end{array}\right.$��
���ACE�ա�CBF��
��AE=CF��
��ͼ2�У����ۣ�EF=$\sqrt{2}$DE���������£�
����DF��
��AE��CE��BF��CE��CD��AB��
���AEC=��BDC=90�㣬
���FCD+��CGD=90�㣬��DAE+��AGE=90�㣬
�ߡ�AGE=��CGD��
���EAD=��FCD��
��CA=CB��
��AD=DB��
��CD=AD=DB��
�ڡ�DAE�͡�DCF�У�
$\left\{\begin{array}{l}{DC=DA}\\{��DCF=��DAE}\\{CF=AE}\end{array}\right.$��
���DCF�ա�DAE��
��DE=DF����CDF=��ADE��
���EDF=��ADC=90�㣬
���EDF�ǵ���ֱ�������Σ�
��EF=$\sqrt{2}$DE��
��2����ͼ3�У����ۣ�$\frac{EF}{DE}$=$\frac{\sqrt{1+{k}^{2}}}{k}$���������£�
����DF��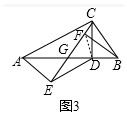
�ߡ�ACD+��BCD=90�㣬��BCD+��CBD=90�㣬
���ACD=��CBD���ߡ�ADC=��CDB��
���ACD�ס�CBD��
��$\frac{AD}{CD}$=$\frac{AC}{BC}$=k��
�ɣ�1����֪����ACE=��CBF���ߡ�AEC=��BFC=90�㣬
���ACE�ס�CBF��
��$\frac{AE}{CF}$=$\frac{AC}{BC}$=k��
��$\frac{AE}{CF}$=$\frac{AD}{CD}$=k���ߡ�DAE=��DCF��
���ADE�ס�CDF��
��$\frac{DE}{DF}$=$\frac{AE}{CF}$=k����ADE=��CDF��
���EDF=��ADC=90�㣬
��DF=m����DE=km��EF=$\sqrt{D{E}^{2}+D{F}^{2}}$=$\sqrt{1+{k}^{2}}$•m��
��$\frac{EF}{DE}$=$\frac{\sqrt{1+{k}^{2}}•m}{km}$=$\frac{\sqrt{1+{k}^{2}}}{k}$��
���� ���⿼�����������ε��ж������ʡ�ȫ�������ε��ж������ʡ����ɶ���������ֱ�������ε����ʵ�֪ʶ������Ĺؼ�����ȷѰ��ȫ�������λ����������ν�����⣬�����п��������ͣ�

 ��������һ���þ�ϵ�д�
��������һ���þ�ϵ�д� Сѧ��10����Ӧ����ϵ�д�
Сѧ��10����Ӧ����ϵ�д�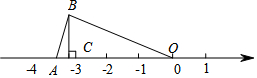 ��ͼ��OA=OB��BC=1���������ϵ�A����ʾ����Ϊ��������
��ͼ��OA=OB��BC=1���������ϵ�A����ʾ����Ϊ��������| A�� | $\sqrt{10}$ | B�� | $\sqrt{5}$ | C�� | $-\sqrt{10}$ | D�� | -3.5 |
 ��ͼ����ABC=��ADC=90�㣬AB=AD��AC��BD�ཻ�ڵ�O����֤��OD=OB��
��ͼ����ABC=��ADC=90�㣬AB=AD��AC��BD�ཻ�ڵ�O����֤��OD=OB�� ��ͼ����֪AD=BC��AC=BD����̽����OA��OB�Ƿ���ȣ�����ȣ���֤����������ȣ���˵�����ɣ�
��ͼ����֪AD=BC��AC=BD����̽����OA��OB�Ƿ���ȣ�����ȣ���֤����������ȣ���˵�����ɣ�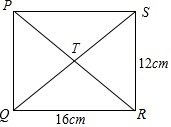 ��ͼ�У�PQRS��һ�������Σ�PR��QS�ཻ��T����
��ͼ�У�PQRS��һ�������Σ�PR��QS�ཻ��T����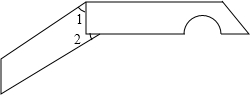 ��ͼ�������������о����Ӵ���С����������һ��ֱ�����Σ���ȥһ����Բ������Ƭ������ƽ�еģ�ת����Ƭʱ���γɡ�1����2�����1+��2=90�㣮
��ͼ�������������о����Ӵ���С����������һ��ֱ�����Σ���ȥһ����Բ������Ƭ������ƽ�еģ�ת����Ƭʱ���γɡ�1����2�����1+��2=90�㣮 ��ͼ��Ϊ���������Ŀ�AB�����ڳ�����ѡһ��O������AO��BO�����AO=18cm��BO=21cm�����ӳ�AO��BO�ֱ�C��D���㣬ʹOC=6cm��OD=7cm�������CD=5cm���������AB���ڣ�������
��ͼ��Ϊ���������Ŀ�AB�����ڳ�����ѡһ��O������AO��BO�����AO=18cm��BO=21cm�����ӳ�AO��BO�ֱ�C��D���㣬ʹOC=6cm��OD=7cm�������CD=5cm���������AB���ڣ�������