题目内容
13.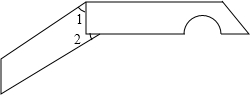 如图,是我们生活中经常接触的小刀,刀柄是一个直角梯形(挖去一个半圆),刀片上下是平行的,转动刀片时会形成∠1、∠2,则∠1+∠2=90°.
如图,是我们生活中经常接触的小刀,刀柄是一个直角梯形(挖去一个半圆),刀片上下是平行的,转动刀片时会形成∠1、∠2,则∠1+∠2=90°.
分析 如图,过点O作OP∥AB,则AB∥OP∥CD.所以根据平行线的性质将(∠1+∠2)转化为(∠AOP+∠POC)来解答即可.
解答  解:如图,过点O作OP∥AB,则∠1=∠AOP.
解:如图,过点O作OP∥AB,则∠1=∠AOP.
∵AB∥CD,
∴OP∥CD,
∴∠2=∠POC,
∵∠AOP+∠POC=90°,
∴∠1+∠2=90°,
故答案为:90°
点评 本题考查了平行线的性质.关键是根据平行线性质定理:
定理1:两直线平行,同位角相等. 定理2:两直线平行,同旁内角互补. 定理3:两直线平行,内错角相等,解答.

练习册系列答案
相关题目
1.要组织一次排球邀请赛,参赛的每两个队之间都要比赛一场,根据场地和时间等条件,赛程计划安排7天,每天安排4场比赛,设比赛组织者应邀请x个队参赛,则x满足的关系式为( )
| A. | x(x+1)=28 | B. | x(x-1)=28×2 | C. | x(x+1)=28 | D. | x(x-1)=28 |
2.运用等式性质进行的变形,不正确的是( )
| A. | 如果a=b,那么a-c=b-c | B. | 如果$\frac{a}{c}=\frac{b}{c}$,那么a=b | ||
| C. | 如果ac2=bc2,那么a=b | D. | 如果a(c2+1)=b(c2+1),那么a=b |
3.在△ABC中,点D、E分别在边AB、AC上,如果AD=2,BD=4,那么由下列条件能够判断DE∥BC的是( )
| A. | $\frac{AE}{AC}=\frac{1}{2}$ | B. | $\frac{DE}{BC}=\frac{1}{3}$ | C. | $\frac{AE}{AC}=\frac{1}{3}$ | D. | $\frac{DE}{BC}=\frac{1}{2}$ |
 已知:如图,AB=CD,AD=BC,P为AC上任一点,过P的直线分别交AD、CB的延长线于E、F.求证:∠E=∠F.
已知:如图,AB=CD,AD=BC,P为AC上任一点,过P的直线分别交AD、CB的延长线于E、F.求证:∠E=∠F.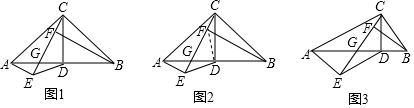
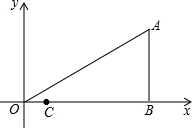 如图,在平面直角坐标系中,已知Rt△ABO的顶点B在x轴正半轴上,∠AOB=30?,OA=2$\sqrt{3}$,C($\frac{1}{2}$,0),P 为OA上的一个动点,
如图,在平面直角坐标系中,已知Rt△ABO的顶点B在x轴正半轴上,∠AOB=30?,OA=2$\sqrt{3}$,C($\frac{1}{2}$,0),P 为OA上的一个动点,