题目内容
1.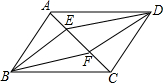 如图,E、F是平行四边形ABCD的对角线AC上的点,AF=CE.
如图,E、F是平行四边形ABCD的对角线AC上的点,AF=CE.(1)求证:四边形BFDE是平行四边形;
(2)若AC=18,BE⊥AC于E,AB=9,BE=7,求AB与CD之间的距离.
分析 (1)连接BD交AC于O;先根据平行四边形的性质得出对角线互相平分OA=OC,OB=OD,再由已知条件得出OE=OF,即可证出四边形BFDE是平行四边形;
(2)根据平行四边形ABCD的面积等于△ABC面积的2倍即可求出结果.
解答 (1)证明:连接BD交AC于O;如图所示: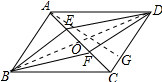 ∵四边形ABCD是平行四边形,
∵四边形ABCD是平行四边形,
∴OA=OC,OB=OD,
∵AF=CE,
∴OE=OF,
∴四边形BFDE是平行四边形;
(2)解:作AG⊥CD于G;
∵BE⊥AC,
∴S△ABC=$\frac{1}{2}$AC×BE,
∴S平行四边形ABCD=2S△ABC=2×$\frac{1}{2}$AC×BE=AC•BE,
又∵S平行四边形ABCD=AB•AG,
∴AB•AG=AC•BE,
∴AG=$\frac{18×7}{9}$=14,
即AB与CD之间的距离为14.
点评 本题考查了平行四边形的判定与性质以及平行四边形面积的计算方法;熟练掌握平行四边形的判定方法和面积之间的关系是解题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
11.若a的倒数仍为a,则a的值是( )
| A. | 1 | B. | 0 | C. | -1 | D. | ±1 |
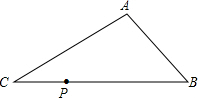 如图,已知点P是Rt△ABC的斜边BC上任意一点,若过点P作直线PD与直角边AB或AC相交于点D,截得的小三角形与△ABC相似,那么D点的位置最多有( )
如图,已知点P是Rt△ABC的斜边BC上任意一点,若过点P作直线PD与直角边AB或AC相交于点D,截得的小三角形与△ABC相似,那么D点的位置最多有( ) 如图,四边形ABCD是正方形,AE垂直于BE,且AE=3,BE=4,阴影部分的面积是19.
如图,四边形ABCD是正方形,AE垂直于BE,且AE=3,BE=4,阴影部分的面积是19.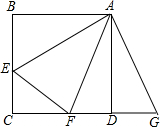 正方形ABCD中,E,F分别是边BC,CD上的点,且∠EAF=45°,将△ABE绕点A逆时针旋转90°,得到△ADG.求证:EF=BE+DF.
正方形ABCD中,E,F分别是边BC,CD上的点,且∠EAF=45°,将△ABE绕点A逆时针旋转90°,得到△ADG.求证:EF=BE+DF.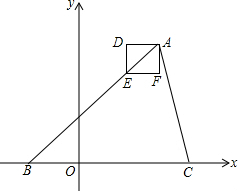 如图,在平面直角坐标系中,△ABC的边BC在x轴上,点A、B的坐标分别为(3,4)(-2,0),边长为$\frac{9}{8}$的正方形ADEF的位置如图所示,且边AD与x轴平行.将正方形ADEF沿平行于y轴方向向下平移$\frac{5}{2}$个单位长度,再沿平行于x轴方向向左平移m(m>0)个单位长度,如果平移后的正方形的顶点E在△ABC的内部,则m的取值范围是0<m<3.40625.
如图,在平面直角坐标系中,△ABC的边BC在x轴上,点A、B的坐标分别为(3,4)(-2,0),边长为$\frac{9}{8}$的正方形ADEF的位置如图所示,且边AD与x轴平行.将正方形ADEF沿平行于y轴方向向下平移$\frac{5}{2}$个单位长度,再沿平行于x轴方向向左平移m(m>0)个单位长度,如果平移后的正方形的顶点E在△ABC的内部,则m的取值范围是0<m<3.40625. 如图所示,三角形AOB绕着点O旋转至三角形A1OB1,若∠AOA1=60°,∠BOA1=28°,则∠A1OB1=32°.
如图所示,三角形AOB绕着点O旋转至三角形A1OB1,若∠AOA1=60°,∠BOA1=28°,则∠A1OB1=32°.