题目内容
9.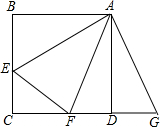 正方形ABCD中,E,F分别是边BC,CD上的点,且∠EAF=45°,将△ABE绕点A逆时针旋转90°,得到△ADG.求证:EF=BE+DF.
正方形ABCD中,E,F分别是边BC,CD上的点,且∠EAF=45°,将△ABE绕点A逆时针旋转90°,得到△ADG.求证:EF=BE+DF.
分析 首先证明FG=BE+DF;其次证明AE=AG,∠EAF=∠FAG,此为解题的关键性结论;证明△EAF≌△GAF,得到EF=FG,即可解决问题.
解答  证明:如图,由题意得:△ABE≌△ADG,
证明:如图,由题意得:△ABE≌△ADG,
∴∠BAE=∠DAG,AE=AG,BE=DG;
∴FG=BE+DF;
∴∠BAE+∠FAD=∠FAD+∠DAG;
∵∠EAF=45°,∠BAD=90°,
∴∠BAE+∠FAD=90°-45°=45°,
∴∠FAG=45°,∠EAF=∠FAG;
在△EAF与△GAF中,
$\left\{\begin{array}{l}{AE=AG}\\{∠EAF=∠GAF}\\{AF=AF}\end{array}\right.$,
∴△EAF≌△GAF(SAS),
∴EF=FG,而FG=BE+DF,
∴EF=BE+DF.
点评 该题主要考查了旋转变换的性质、正方形的性质、全等三角形的判定及其性质等知识点及其应用问题;应牢固掌握旋转变换的性质等知识点;解题的关键是抓住旋转变换过程中的不变量.

练习册系列答案
相关题目
20.若A(x1,y1),B(x2,y2),C(x3,y3)是反比例函数y=$\frac{5}{x}$图象上的点,且x1<x2<0<x3,则y1,y2,y3的大小关系正确的是( )
| A. | y3>y1>y2 | B. | y1>y2>y3 | C. | y2>y1>y3 | D. | y3>y2>y1 |
4.下列图案是轴对称图形的有( )个.


| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
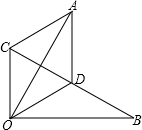 如图,△OBD中,OD=BD,△OBD绕点O逆时针旋转一定角度后得到△OAC,此时B,D,C三点正好在一条直线上,且点D是BC的中点.
如图,△OBD中,OD=BD,△OBD绕点O逆时针旋转一定角度后得到△OAC,此时B,D,C三点正好在一条直线上,且点D是BC的中点. 如图所示,直线AB,CD相交于O,若∠1=$\frac{2}{7}$∠2,则∠2=140度.
如图所示,直线AB,CD相交于O,若∠1=$\frac{2}{7}$∠2,则∠2=140度.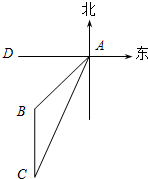 2014年3月8日凌晨2点40分,马来西亚航空公司的一架载有239人的波音777-200飞机与管制中心失去联系,我国救援船舰马上开展搜救工作,一艘搜救船与某日上午8点在A处望见西南方向有一座灯塔B(如图),此时测得船和灯塔相距60$\sqrt{2}$海里,船以每小时30海里的速度向南偏西24°的方向航行到C处,这时望见灯塔在船的正北方向(参考数据:sin24°≈0.4,cos24°≈0.9).
2014年3月8日凌晨2点40分,马来西亚航空公司的一架载有239人的波音777-200飞机与管制中心失去联系,我国救援船舰马上开展搜救工作,一艘搜救船与某日上午8点在A处望见西南方向有一座灯塔B(如图),此时测得船和灯塔相距60$\sqrt{2}$海里,船以每小时30海里的速度向南偏西24°的方向航行到C处,这时望见灯塔在船的正北方向(参考数据:sin24°≈0.4,cos24°≈0.9).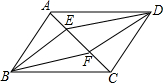 如图,E、F是平行四边形ABCD的对角线AC上的点,AF=CE.
如图,E、F是平行四边形ABCD的对角线AC上的点,AF=CE.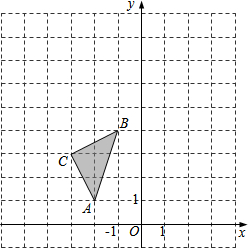 如图,在平面直角坐标系中,△ABC的三个顶点坐标分别为A(-2,1),B(-1,4),C(-3,3).
如图,在平面直角坐标系中,△ABC的三个顶点坐标分别为A(-2,1),B(-1,4),C(-3,3).