题目内容
15. a,b,c在数轴上的对应点如图所示,化简$\sqrt{(a-b)^{2}}$+|c-b|-($\root{3}{a+c}$)3.
a,b,c在数轴上的对应点如图所示,化简$\sqrt{(a-b)^{2}}$+|c-b|-($\root{3}{a+c}$)3.
分析 根据数轴上点的位置判断出a-b,c-b,以及a+c的正负,利用平方根、立方根定义,以及绝对值的代数意义化简即可得到结果.
解答 解:根据数轴上点的位置得:a<b<0<c,
且|a|>|b|>|c|,
∴a-b<0,c-b>0,a+c<0,
则原式=|a-b|+|c-b|-(a+c)=b-a+c-b-a-c=-2a.
点评 此题考查了实数的运算,绝对值,以及实数与数轴,熟练掌握绝对值的代数意义是解本题的关键.

练习册系列答案
相关题目
3.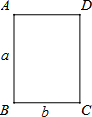 如图,矩形ABCD中,AB=a,BC=b,a>b,以AB边为轴将矩形绕其旋转一周形成圆柱体甲,再以BC边为轴将矩形绕其旋转一周形成圆柱体乙,记两个圆柱体的体积分别为V甲、V乙,侧面积分别为S甲、S乙,则下列式子正确的是( )
如图,矩形ABCD中,AB=a,BC=b,a>b,以AB边为轴将矩形绕其旋转一周形成圆柱体甲,再以BC边为轴将矩形绕其旋转一周形成圆柱体乙,记两个圆柱体的体积分别为V甲、V乙,侧面积分别为S甲、S乙,则下列式子正确的是( )
 如图,矩形ABCD中,AB=a,BC=b,a>b,以AB边为轴将矩形绕其旋转一周形成圆柱体甲,再以BC边为轴将矩形绕其旋转一周形成圆柱体乙,记两个圆柱体的体积分别为V甲、V乙,侧面积分别为S甲、S乙,则下列式子正确的是( )
如图,矩形ABCD中,AB=a,BC=b,a>b,以AB边为轴将矩形绕其旋转一周形成圆柱体甲,再以BC边为轴将矩形绕其旋转一周形成圆柱体乙,记两个圆柱体的体积分别为V甲、V乙,侧面积分别为S甲、S乙,则下列式子正确的是( )| A. | V甲>V乙,S甲=S乙 | B. | V甲<V乙,S甲=S乙 | C. | V甲=V乙,S甲=S乙 | D. | V甲>V乙,S甲<S乙 |
4.有一个三位数,现将它最左边的数字移至最右边所得到的数比原来的数小144;而由它的十位数字与个位数字所组成的两位数除以百位数字,商是7,余数是4.如果设这个三位数的百位为x,十位与个位数字组成的两位数为y,可得方程组是( )
| A. | $\left\{\begin{array}{l}{(100x+y)-(100y+x)=144}\\{y=7x+4}\end{array}\right.$ | B. | $\left\{\begin{array}{l}{(100x+y)-(10y+x)=144}\\{y=7x+4}\end{array}\right.$ | ||
| C. | $\left\{\begin{array}{l}{(10y+x)-(100x+y)=144}\\{y=7x+4}\end{array}\right.$ | D. | $\left\{\begin{array}{l}{(100x+y)-(10x+y)=144}\\{y=7x+4}\end{array}\right.$ |
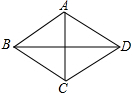 如图,已知菱形ABCD的两条对角线AC、BD分别长6cm、8cm,则它的周长是20cm,面积是24cm2.
如图,已知菱形ABCD的两条对角线AC、BD分别长6cm、8cm,则它的周长是20cm,面积是24cm2.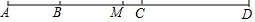 已知,如图B,C两点把线段AD分成2:4:3三部分,M是AD的中点,CD=6cm,则线段AD的长为多少厘米?
已知,如图B,C两点把线段AD分成2:4:3三部分,M是AD的中点,CD=6cm,则线段AD的长为多少厘米? 如图,已知AB∥DE,D是BC的中点,∠A=∠E,证明:△ABD≌△EDC.
如图,已知AB∥DE,D是BC的中点,∠A=∠E,证明:△ABD≌△EDC.