题目内容
10.|x-1|+|x-2|+|x-3|+…+|x-2016|的最小值=1016064.分析 根据绝对值几何意义求最小值$\left\{\begin{array}{l}零点个数为奇数,取中间点\\ 零点个数为偶数,取中间段\end{array}\right.$,进而求出答案.
解答 解:如图,
∵根据绝对值几何意义,且零点个数为偶数,
∴当1008≤x≤1009时,原式取得最小值,最小值为
(1+2+3+…+1007)+(1+2+3+…+1008)=1016064.
故答案为:1016064.
点评 此题主要考查了绝对值,正确理解绝对值的性质得出1008≤x≤1009时代数式取值最小是解题关键.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
20.按如图所示的程序计算,若开始输入的n值为 $\sqrt{2}$,则最后输出的结果是( ) 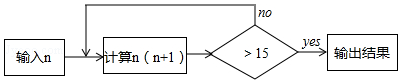

| A. | 14 | B. | 16 | C. | 8+5$\sqrt{2}$ | D. | 14+$\sqrt{2}$ |
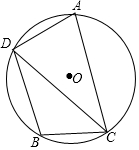 如图,⊙O中,$\widehat{AB}$=$\widehat{AC}$,D为$\widehat{AB}$上任意一点,若cos∠BDC=$\frac{3}{4}$,求tan∠ADC的值.
如图,⊙O中,$\widehat{AB}$=$\widehat{AC}$,D为$\widehat{AB}$上任意一点,若cos∠BDC=$\frac{3}{4}$,求tan∠ADC的值.
 a,b,c在数轴上的对应点如图所示,化简$\sqrt{(a-b)^{2}}$+|c-b|-($\root{3}{a+c}$)3.
a,b,c在数轴上的对应点如图所示,化简$\sqrt{(a-b)^{2}}$+|c-b|-($\root{3}{a+c}$)3.