题目内容
15．计算：sin245°+cos245°+$\frac{cos30°-sin30°}{tan60°-cot45°}$+tan30°•cot30°．分析 根据特殊角三角函数值，可得答案．
解答 解：原式=（$\frac{\sqrt{2}}{2}$）2+（$\frac{\sqrt{2}}{2}$）2+$\frac{\frac{\sqrt{3}}{2}-\frac{1}{2}}{\sqrt{3}-1}$+$\frac{\sqrt{3}}{3}$×$\sqrt{3}$
=$\frac{1}{2}$+$\frac{1}{2}$+$\frac{1}{2}$+1
=$\frac{5}{2}$．
点评 本题考查了特殊角三角函数值，熟记特殊角三角函数值是解题关键．
练习册系列答案
名校课堂系列答案
相关题目
14．某乒乓球馆有两种计费方案，如下图表．李强和同学们打算周末去此乒乓球馆连续打球4小时，经服务生测算后，告知他们包场计费方案会比人数计费方案便宜，则他们参与包场的人数至少为（ ）
| 包场计费：包场每场每小时50元，每人须另付入场费5元 |
| 人数计费：每人打球2小时20元，接着续打球每人每小时6元 |
| A． | 9 | B． | 8 | C． | 7 | D． | 6 |
6．
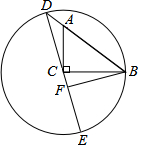如图，直角△ABC中，∠ACB=90°，AC=3，BC=4，以C为圆心BC为半径画圆交BA延长线于点D，连接DC并延长交圆C于点E，过点B作DE的垂线BF，垂足为点F，那么线段BF的长度为（ ）
如图，直角△ABC中，∠ACB=90°，AC=3，BC=4，以C为圆心BC为半径画圆交BA延长线于点D，连接DC并延长交圆C于点E，过点B作DE的垂线BF，垂足为点F，那么线段BF的长度为（ ）| A． | $\frac{18}{5}$ | B． | 3.5 | C． | $\frac{19}{5}$ | D． | $\frac{96}{25}$ |
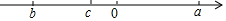有理数a，b，c在数轴上的位置如图所示，且|a|=|b|．
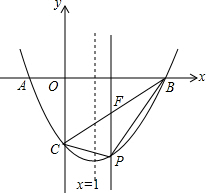如图，在平面直角坐标系中，点A、C的坐标分别为（-1，0）、（0，-6）点B在x轴上．已知某二次函数的图象经过A、B、C三点，且它的对称轴为直线x=1，点P为直线BC下方的二次函数图象上的一个动点（点P与B、C不重合），过点P作y轴的平行线交BC于点F．