题目内容
15.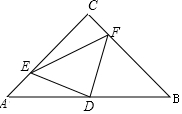 如图,在△ABC中,AC=BC,∠C=90°,D是AB的中点,AE=CF.求证:△DEF是等腰直角三角形(提示:用到三线合一)
如图,在△ABC中,AC=BC,∠C=90°,D是AB的中点,AE=CF.求证:△DEF是等腰直角三角形(提示:用到三线合一)
分析 连接CD,由等腰直角三角形的性质得出CD=$\frac{1}{2}$BA=AD=BD,∠A=∠DCF=45°,由SAS证明证明△ADE≌△CDF,可得DF=DE,∠CDF=∠ADE,即可求得∠EDF=90°,即可得出结论.
解答 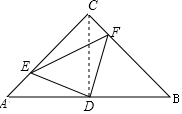 证明:连接CD,
证明:连接CD,
∵AC=BC,∠C=90°,D是AB的中点,
∴AD=CD,∠A=∠BCD=45°,∠ADC=∠CDB=90°,
在△ADE与△CDF中,$\left\{\begin{array}{l}{AE=CF}\\{∠A=∠DCF}\\{AD=CD}\end{array}\right.$,
∴△ADE≌△CDF,
∴∠ADE=∠CDF,DE=DF,
∴∠CDF+∠CDE=90°,
∴∠EDF=90°,
∴,△DEF是等腰直角三角形.
点评 本题考查了全等三角形的判定与性质、等腰直角三角形的性质;熟练掌握等腰直角三角形的性质,证明三角形全等是解决问题的关键.

练习册系列答案
相关题目
5.正比例函数y=kx的图象经过直线y=x+1与y=3x+5的交点,那么y=kx的图象位于( )
| A. | 第一、三象限 | B. | 第二、四象限 | C. | 第一、二象限 | D. | 第一、二、三象限 |
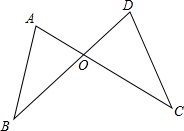 如图,已知AB,CD相交于点O,且AB=DC,AC=DB,∠A=65°,∠ACD=45°.
如图,已知AB,CD相交于点O,且AB=DC,AC=DB,∠A=65°,∠ACD=45°. 已知AB=AD,BC=DC.求证:AC平分∠BAD.
已知AB=AD,BC=DC.求证:AC平分∠BAD.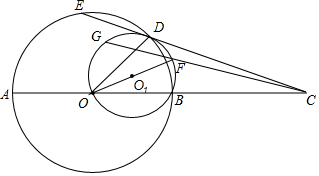 已知:AB是⊙O的直径,C为AB延长线上的一点,过点C作⊙O的割线,与⊙O交于D、E两点,OF是△BOD的外接圆O1的直径,连接CF并延长交⊙O1于点G.求证:O、A、E、G四点共圆.
已知:AB是⊙O的直径,C为AB延长线上的一点,过点C作⊙O的割线,与⊙O交于D、E两点,OF是△BOD的外接圆O1的直径,连接CF并延长交⊙O1于点G.求证:O、A、E、G四点共圆.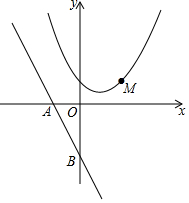 直线y=-$\frac{4}{3}$x-4与x轴交于点A,与y轴交于点B,抛物线y=x2-4x+5上的一点M(3,2).
直线y=-$\frac{4}{3}$x-4与x轴交于点A,与y轴交于点B,抛物线y=x2-4x+5上的一点M(3,2).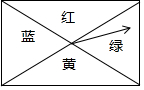 如图,一块长宽不等的矩形木板,连接对角线后被分成4个区域,分别涂上红、黄、蓝、绿四色,木板中间装有指针,指针转动停止后,下面两个结论:
如图,一块长宽不等的矩形木板,连接对角线后被分成4个区域,分别涂上红、黄、蓝、绿四色,木板中间装有指针,指针转动停止后,下面两个结论: