题目内容
2.已知关于x的方程x2-(k+1)x+$\frac{1}{4}$k2+1=0.(1)若方程有两个不相等的实数根,求k的取值范围;
(2)若方程的两根x1,x2恰好是一个矩形两邻边的长,且矩形的对角线长为$\sqrt{5}$,求k.
分析 (1)由根的判别式△<0得到关于k的一元一次不等式,通过解不等式求得k的取值范围;
(2)设方程的两根为x1,x2,依题意x12+x22=$\sqrt{5}$,又根据根与系数的关系可以得到x1+x2=k+1,x1•x2=$\frac{1}{4}$k2+1,而x12+x22=(x1+x2)2-2x1•x2,这样利用这些等式变形即可求解.
解答 解:(1)依题意△=[-(k+1)]2-4×1×($\frac{1}{4}$k2+1)=2k-3≥0,
∴k≥$\frac{3}{2}$;
(2)设方程的两根为x1,x2,
依题意x12+x22=($\sqrt{5}$)2,
∵x1+x2=k+1,x1•x2=$\frac{1}{4}$k2+1,
∴x12+x22=(x1+x2)2-2x1•x2=(k+1)2-2($\frac{1}{4}$k2+1)=5,
整理得:k2+4k-12=0,
∴k=-6或k=2,
当k=-6时,x1+x2=k+1=-5<0,舍去,
∴k=2.
点评 此题主要考查了一元二次方程的根的判别式和根与系数的关系,首先利用判别式是非负数确定k的取值范围,然后利用各与系数的关系确定k的值.

练习册系列答案
相关题目
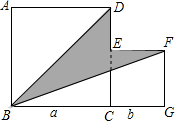 如图,正方形ABCD与正方形EFGC的边长分别为a、b,B、C、G三点在同一直线上,连结BD、BF.
如图,正方形ABCD与正方形EFGC的边长分别为a、b,B、C、G三点在同一直线上,连结BD、BF.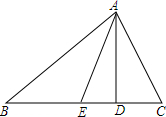 如图,在△ABC中,∠B=50°,∠C=70°,AD是高,AE是角平分线,
如图,在△ABC中,∠B=50°,∠C=70°,AD是高,AE是角平分线,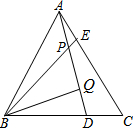 如图,△ABC为等边三角形,AE=CD,AD、BE相交于点P,BQ⊥AD于Q,PQ=4,PE=1
如图,△ABC为等边三角形,AE=CD,AD、BE相交于点P,BQ⊥AD于Q,PQ=4,PE=1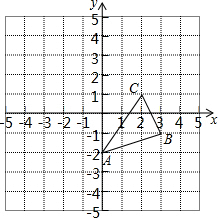 将图中的△ABC作下列变换,画出相应的图形;
将图中的△ABC作下列变换,画出相应的图形;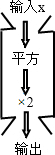 如图是一组数值转换机,若它输出的结果为18,则输入值为±3.
如图是一组数值转换机,若它输出的结果为18,则输入值为±3. 已知:如图,AB=AC,BD⊥AC于D,请探究∠DBC与∠A的数量关系并说明理由.
已知:如图,AB=AC,BD⊥AC于D,请探究∠DBC与∠A的数量关系并说明理由.