题目内容
11．有一个整式减去（xy-2yz+3xz）的题目，小春同学误看成加法了，得到的答案是2yz-3xz+2xy．假如小春同学没看错，原来题目正确解答是什么？分析 先求出整式的表达式，再由整式加减的法则求出结论即可．
解答 解：原整式为（2yz-3zx+2xy）-（xy-2yz+3xz）
=xy+4yz-6xz．
则原题正解：（xy+4yz-6xz）-（xy-2yz+3xz）
=6yz-9xz．
点评 本题考查的是整式的加减，熟知整式的加减实质上就是合并同类项是解答此题的关键．
练习册系列答案
相关题目
1．下列分式化简正确的是（ ）
| A． | $\frac{{{x^2}+x}}{{{x^2}+2}}=\frac{x}{2}$ | B． | $\frac{{{x^2}-2x}}{2y-xy}=\frac{x}{y}$ | ||
| C． | $\frac{{{x^2}-9}}{{{x^2}-6x+9}}=\frac{x+3}{x-3}$ | D． | $\frac{x+2}{{{x^2}+4}}=\frac{1}{x+2}$ |
6．若多项式3x2y2-2xy-x+8y与某多项式的差为x2-2x+1，则这个多项式为（ ）
| A． | 3x2y2-2xy-x2+8y-3x-1 | B． | 3x2y2-2xy-x2+8y-3x+1 | ||
| C． | 3x2y2-2xy-x2+8y+x+1 | D． | 3x2y2-2xy-x2+8y+x-1 |
20．
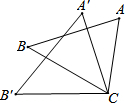如图，△ACB≌△A′B′C′，AC与A′C，是对应边，∠A=60°，∠ACB=70°，则∠B′的度数为（ ）
如图，△ACB≌△A′B′C′，AC与A′C，是对应边，∠A=60°，∠ACB=70°，则∠B′的度数为（ ）| A． | 70° | B． | 60° | C． | 50° | D． | 40° |
