题目内容
12．
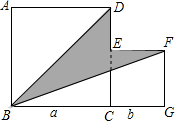如图，正方形ABCD与正方形EFGC的边长分别为a、b，B、C、G三点在同一直线上，连结BD、BF．（1）求阴影部分图形的面积（用含a、b的代数式表示）．
（2）若a+b=8，ab=15，则阴影部分图形的面积为$\frac{19}{2}$．
分析 （1）由阴影部分面积=正方形ABCD面积+正方形EFGH面积-三角形ABD面积-三角形BGF面积，列出关系式，计算即可；
（2）由（1）的结果变形后，将a+b与ab的值代入计算即可求出值．
解答 解：（1）S阴影=S正方形ABCD+S正方形EFGC-S△ABD-S△BGF
=a2+b2-$\frac{1}{2}$a2-$\frac{1}{2}$b（a+b）
=a2+b2-$\frac{1}{2}$a2-$\frac{1}{2}$ab-$\frac{1}{2}$b2=$\frac{1}{2}$a2+$\frac{1}{2}$b2-$\frac{1}{2}$ab；
（2）∵a+b=8，ab=15，
∴阴影部分的面积为$\frac{1}{2}$[（a+b）2-3ab]=$\frac{1}{2}$×（64-45）=$\frac{19}{2}$，
故答案为：$\frac{19}{2}$
点评 此题考查了整式的混合运算，熟练掌握运算法则是解本题的关键．
练习册系列答案
相关题目
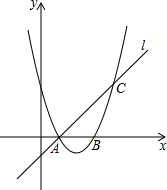如图，已知抛物线y=ax2+bx+3与x轴交于A，B两点，过点A的直线l与抛物线交于点C，其中A点的坐标是（1，0），C点的坐标是（4，3）．
3．-（-1）3=（ ）
| A． | -3 | B． | -1 | C． | 3 | D． | 1 |
20．若（x+2）2+|y-1|=0，则-x2y2的值为（ ）
| A． | 4 | B． | -4 | C． | 8 | D． | -8 |
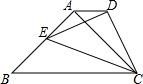如图，已知：等腰Rt△ABC中，∠BAC=90°，BC=2，E为边AB上任意一点，以CE为斜边作等腰Rt△CDE，连接AD，下列说法：
按要求画图，用尺规画图，保留痕迹．
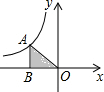如图，点A在反比例函数y=$\frac{k}{x}$的图象上，AB垂直x轴于B，若S△AOB=2，则这个反比例函数的解析式为y=-$\frac{4}{x}$．
1．下列分式化简正确的是（ ）
| A． | $\frac{{{x^2}+x}}{{{x^2}+2}}=\frac{x}{2}$ | B． | $\frac{{{x^2}-2x}}{2y-xy}=\frac{x}{y}$ | ||
| C． | $\frac{{{x^2}-9}}{{{x^2}-6x+9}}=\frac{x+3}{x-3}$ | D． | $\frac{x+2}{{{x^2}+4}}=\frac{1}{x+2}$ |