题目内容
10.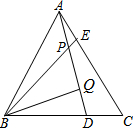 如图,△ABC为等边三角形,AE=CD,AD、BE相交于点P,BQ⊥AD于Q,PQ=4,PE=1
如图,△ABC为等边三角形,AE=CD,AD、BE相交于点P,BQ⊥AD于Q,PQ=4,PE=1(1)求证:∠BPQ=60°;(提示:利用三角形全等、外角的性质)
(2)求BE的长.
分析 (1)由△ABC为等边三角形,AE=CD,可以推出△BAE≌△ACD,再根据全等三角形的对应角相等,三角形的外角等于和它不相邻的两个内角的和,从而可以解答本题.
(2)根据BQ⊥AD于Q,PQ=4,PE=1,∠BPQ=60°,可以得到BP的长,从而得到BE的长.
解答 (1)证明:∵△ABC为等边三角形,
∴AB=AC,∠BAE=∠ACD=60°.
在△BAE和△ACD中
$\left\{\begin{array}{l}{AB=AC}\\{∠BAE=∠ACD}\\{AE=CD}\end{array}\right.$
∴△BAE≌△ACD(SAS).
∴∠ABE=∠CAD.
∴∠ABE+∠BAP=∠CAD+∠BAP=∠BAE=60°.
∵∠BPQ=∠ABE+∠BAP,
∴∠BPQ=60°.
(2)解:∵BQ⊥AD于Q,PQ=4,∠BPQ=60°,
∴∠BQP=90°,∠PBQ=30°.
∴BP=2PQ=8.
∵PE=1,BE=BP+PE.
∴BE=8+1=9.
点评 本题考查三角形全等的证明、直角三角形中30°角所对的直角边和斜边的关系,解答本题的关键是找出所求问题需要的条件.需要注意的是证明题要先写证明,解答题要写解.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
20.若(x+2)2+|y-1|=0,则-x2y2的值为( )
| A. | 4 | B. | -4 | C. | 8 | D. | -8 |
1.下列分式化简正确的是( )
| A. | $\frac{{{x^2}+x}}{{{x^2}+2}}=\frac{x}{2}$ | B. | $\frac{{{x^2}-2x}}{2y-xy}=\frac{x}{y}$ | ||
| C. | $\frac{{{x^2}-9}}{{{x^2}-6x+9}}=\frac{x+3}{x-3}$ | D. | $\frac{x+2}{{{x^2}+4}}=\frac{1}{x+2}$ |
20.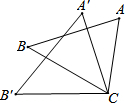 如图,△ACB≌△A′B′C′,AC与A′C,是对应边,∠A=60°,∠ACB=70°,则∠B′的度数为( )
如图,△ACB≌△A′B′C′,AC与A′C,是对应边,∠A=60°,∠ACB=70°,则∠B′的度数为( )
 如图,△ACB≌△A′B′C′,AC与A′C,是对应边,∠A=60°,∠ACB=70°,则∠B′的度数为( )
如图,△ACB≌△A′B′C′,AC与A′C,是对应边,∠A=60°,∠ACB=70°,则∠B′的度数为( )| A. | 70° | B. | 60° | C. | 50° | D. | 40° |
 如图,在平面直角坐标系中,抛物线y=ax2+bx-4与x轴的一个交点为A(2,0),与y轴的交点为C,对称轴是x=-3,对称轴与x轴交于点B.
如图,在平面直角坐标系中,抛物线y=ax2+bx-4与x轴的一个交点为A(2,0),与y轴的交点为C,对称轴是x=-3,对称轴与x轴交于点B. 如图,AC,BD相交于O,∠A=∠D,AB=DC.
如图,AC,BD相交于O,∠A=∠D,AB=DC.