题目内容
13.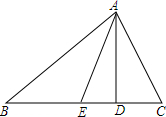 如图,在△ABC中,∠B=50°,∠C=70°,AD是高,AE是角平分线,
如图,在△ABC中,∠B=50°,∠C=70°,AD是高,AE是角平分线,(1)∠BAC=60°,∠DAC=20°.(填度数)
(2)求∠EAD的度数.
分析 (1)根据三角形内角和定理求出∠BAC的度数,根据高的概念求出∠DAC的度数;
(2)根据角平分线的定义求出∠EAC的度数,计算即可.
解答 解:(1)∠BAC=60°,∠DAC=20°,
在△ABC中∠B=50°,∠C=70°,
∠BAC=180°-∠B-∠C=60°,
∵AD是高,∠C=70°,
∴∠DAC=90°-70°=20°,
故答案为:60°;20°;
(2)∵AE是角平分线,
∴∠EAC=$\frac{1}{2}$∠BAC=30°
又∵AD是高,
∴∠DAC+∠C=90°,
∠DAC=90°-70°=20°,
∴∠EAD=∠EAC-∠DAC=10°.
点评 本题考查的是三角形的角平分线、中线和高以及三角形内角和定理,掌握三角形的角平分线、中线和高的概念和性质是解题的关键,注意三角形内角和等于180°.

练习册系列答案
相关题目
3.-(-1)3=( )
| A. | -3 | B. | -1 | C. | 3 | D. | 1 |
1.下列分式化简正确的是( )
| A. | $\frac{{{x^2}+x}}{{{x^2}+2}}=\frac{x}{2}$ | B. | $\frac{{{x^2}-2x}}{2y-xy}=\frac{x}{y}$ | ||
| C. | $\frac{{{x^2}-9}}{{{x^2}-6x+9}}=\frac{x+3}{x-3}$ | D. | $\frac{x+2}{{{x^2}+4}}=\frac{1}{x+2}$ |
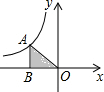 如图,点A在反比例函数y=$\frac{k}{x}$的图象上,AB垂直x轴于B,若S△AOB=2,则这个反比例函数的解析式为y=-$\frac{4}{x}$.
如图,点A在反比例函数y=$\frac{k}{x}$的图象上,AB垂直x轴于B,若S△AOB=2,则这个反比例函数的解析式为y=-$\frac{4}{x}$. 如图,在平面直角坐标系中,抛物线y=ax2+bx-4与x轴的一个交点为A(2,0),与y轴的交点为C,对称轴是x=-3,对称轴与x轴交于点B.
如图,在平面直角坐标系中,抛物线y=ax2+bx-4与x轴的一个交点为A(2,0),与y轴的交点为C,对称轴是x=-3,对称轴与x轴交于点B.


