题目内容
直线l1:y=x+4与x轴交于点A,直线l2:y=-2x+12与x轴交于点B,以AB为直径作⊙M,判断点D(5,3)是否在⊙M上.
考点:直线与圆的位置关系,点与圆的位置关系
专题:计算题
分析:先根据x轴上点的坐标特征确定A(-4,0),B(6,0),再求出AB的中点M的坐标(1,0),且MA=5,然后根据两点间的距离公式计算出MD,再利用点与圆的位置关系进行判断.
解答:解:把y=0代入y=x+4得x+4=0,解得x=-4,则A(-4,0);把y=0代入y=-2x+12得-2x+12=0,解得x=6,则B(6,0),
因为AB为⊙M的直径,
所以M(1,0),MA=5,
而MD=
=5,
即点D到M的距离等于圆的半径,
所以D(5,3)在⊙M上.
因为AB为⊙M的直径,
所以M(1,0),MA=5,
而MD=
| (5-1)2+32 |
即点D到M的距离等于圆的半径,
所以D(5,3)在⊙M上.
点评:本题考查了直线和圆的位置关系:设⊙O的半径为r,圆心O到直线l的距离为d:直线l和⊙O相交?d<r;直线l和⊙O相切?d=r;直线l和⊙O相离?d>r.也考查了点与圆的位置关系.

练习册系列答案
 课堂全解字词句段篇章系列答案
课堂全解字词句段篇章系列答案 步步高口算题卡系列答案
步步高口算题卡系列答案 点睛新教材全能解读系列答案
点睛新教材全能解读系列答案
相关题目
 如图,已知在△ADC中,∠C=90°,AB⊥AC,D、E、B在一直线上,BE=2AD,求证:∠ADE=2∠EDC.
如图,已知在△ADC中,∠C=90°,AB⊥AC,D、E、B在一直线上,BE=2AD,求证:∠ADE=2∠EDC. 如图,平面直角坐标系中,矩形OABC的对角线AC=12,∠ACO=30°
如图,平面直角坐标系中,矩形OABC的对角线AC=12,∠ACO=30° 如图,正方形的棱长为3厘米,把所有的面分成3×3个小正方形,起边长都为1厘米,若一只蚂每秒爬行2.5厘米,则它下底面A点沿表面爬行至右侧面B点,最少要花
如图,正方形的棱长为3厘米,把所有的面分成3×3个小正方形,起边长都为1厘米,若一只蚂每秒爬行2.5厘米,则它下底面A点沿表面爬行至右侧面B点,最少要花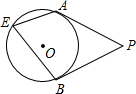 如图,PA,PB分别切⊙O于点A,B,点E是⊙O上一点,且∠AEB=50°,则∠P=
如图,PA,PB分别切⊙O于点A,B,点E是⊙O上一点,且∠AEB=50°,则∠P=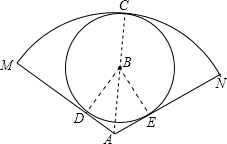 如图,∠MAN=120°,⊙B的半径为r,⊙B与
如图,∠MAN=120°,⊙B的半径为r,⊙B与