题目内容
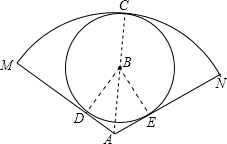 如图,∠MAN=120°,⊙B的半径为r,⊙B与
如图,∠MAN=120°,⊙B的半径为r,⊙B与 |
| MN |
 |
| MN |
考点:切线的性质,弧长的计算
专题:
分析:连接AC,BE,则AC一定经过点B,则BE⊥AN,在直角△ABE中,利用直角三角形的性质求得AB的长,则弧MN的半径即可求得,然后利用弧长公式即可求解.
解答: 解:如图,连接AC,BE,则AC一定经过点B,∠BAE=
解:如图,连接AC,BE,则AC一定经过点B,∠BAE=
∠MAN=60°,BE⊥AN.
∵在直角△ABE中,BE=r,
∴AB=
BE=
r,
∴AC=AB+BC=
r+r=
r,
则
的长是:
=
πr.
 解:如图,连接AC,BE,则AC一定经过点B,∠BAE=
解:如图,连接AC,BE,则AC一定经过点B,∠BAE=| 1 |
| 2 |
∵在直角△ABE中,BE=r,
∴AB=
2
| ||
| 3 |
2
| ||
| 3 |
∴AC=AB+BC=
2
| ||
| 3 |
2
| ||
| 3 |
则
 |
| MN |
120π×
| ||||
| 180 |
4
| ||
| 9 |
点评:本题考查弧长公式以及切线的性质,运用切线的性质来进行计算或论证,常通过作辅助线连接圆心和切点,利用垂直构造直角三角形解决有关问题.

练习册系列答案
相关题目
 已知x2=3,那么在数轴上与实数x对应的点可能是
已知x2=3,那么在数轴上与实数x对应的点可能是 如图,以等腰Rt△ABC的直角顶点A作两个同心圆,大圆过B、C两点,小圆与斜边BC相切于点D,若圆环(图中阴影部分)的面积为16πcm2,则AB=
如图,以等腰Rt△ABC的直角顶点A作两个同心圆,大圆过B、C两点,小圆与斜边BC相切于点D,若圆环(图中阴影部分)的面积为16πcm2,则AB=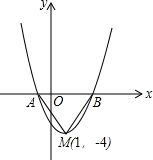 如图是二次函数y=(x+m)2+k的图象,其顶点坐标为M(1,-4).
如图是二次函数y=(x+m)2+k的图象,其顶点坐标为M(1,-4). 如图,等腰梯形ABCD,AD∥BC,BD平分∠ABC,∠A=120°.若梯形的周长为10,则AD的长为
如图,等腰梯形ABCD,AD∥BC,BD平分∠ABC,∠A=120°.若梯形的周长为10,则AD的长为