题目内容
OAB是圆心角为60°的扇形,圆O′内切于扇形OAB,且圆O′的面积为16π,若用这个扇形做成一个圆锥的侧面,求这个圆锥的高及表面积.
考点:圆锥的计算
专题:计算题
分析:连结OO′交弧AB于C,作O′D⊥OB,如图,扇形OAB的半径为R,圆O′的半径为r,根据圆的面积公式可计算出r=4,再利用两圆相切和切线的性质得OC=R,O′D=O′C=4,在Rt△OO′D中,计算出OO′=2O′D=8,则OC=12,设圆锥的底面圆的半径为a,根据弧长公式得到2πa=
,解得a=2,然后利用勾股定理计算这个圆锥的高;根据扇形的面积公式计算这个圆锥的表面积.
| 60•π•12 |
| 180 |
解答:解: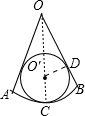 连结OO′交弧AB于C,作O′D⊥OB,如图,扇形OAB的半径为R,圆O′的半径为r,
连结OO′交弧AB于C,作O′D⊥OB,如图,扇形OAB的半径为R,圆O′的半径为r,
∵圆O′的面积为16π
∴πr2=16π,解得r=4,
∵圆O′内切于扇形OAB,
∴OC=R,O′D=O′C=4,
∵∠AOB=60°,
∴∠O′OD=30°,
在Rt△OO′D中,OO′=2O′D=8,
∴OC=8+4=12,
设圆锥的底面圆的半径为a,
2πa=
,解得a=2,
∴这个圆锥的高=
=2
,
这个圆锥的表面积=π•22+
•2π•2•12=28π.
 连结OO′交弧AB于C,作O′D⊥OB,如图,扇形OAB的半径为R,圆O′的半径为r,
连结OO′交弧AB于C,作O′D⊥OB,如图,扇形OAB的半径为R,圆O′的半径为r,∵圆O′的面积为16π
∴πr2=16π,解得r=4,
∵圆O′内切于扇形OAB,
∴OC=R,O′D=O′C=4,
∵∠AOB=60°,
∴∠O′OD=30°,
在Rt△OO′D中,OO′=2O′D=8,
∴OC=8+4=12,
设圆锥的底面圆的半径为a,
2πa=
| 60•π•12 |
| 180 |
∴这个圆锥的高=
| 122-22 |
| 35 |
这个圆锥的表面积=π•22+
| 1 |
| 2 |
点评:本题考查了圆锥的计算:圆锥的侧面展开图为一扇形,这个扇形的弧长等于圆锥底面的周长,扇形的半径等于圆锥的母线长.也考查了勾股定理和两圆相切的性质.

练习册系列答案
 小学夺冠AB卷系列答案
小学夺冠AB卷系列答案
相关题目

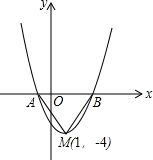 如图是二次函数y=(x+m)2+k的图象,其顶点坐标为M(1,-4).
如图是二次函数y=(x+m)2+k的图象,其顶点坐标为M(1,-4).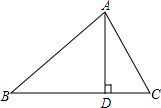 如图,在△ABC中,∠C=60°,AD⊥BC,垂足为D.若CD=
如图,在△ABC中,∠C=60°,AD⊥BC,垂足为D.若CD=