题目内容
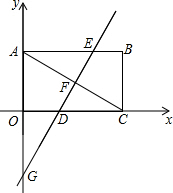 如图,平面直角坐标系中,矩形OABC的对角线AC=12,∠ACO=30°
如图,平面直角坐标系中,矩形OABC的对角线AC=12,∠ACO=30°(1)求B、C两点的坐标;
(2)过点G(0,-6)作GF⊥AC,垂足为F,直线GF分别交AB、OC于点E、D,求直线DE的解析式;
(3)在(2)的条件下,若点M在直线DE上,平面内是否存在点P,使以O、F、M、P为顶点的四边形是菱形?若存在,请直接写出点P的坐标;若不存在,请说明理由.
考点:一次函数综合题
专题:
分析:(1)利用三角函数求得OA以及OC的长度,则C、B的坐标即可得到;
(2)先求出直线DE的斜率,设直线DE的解析式是y=
x+b,再把点G代入求出b的值即可;
(3)分当FM是菱形的边和当OF是对角线两种情况进行讨论.利用三角函数即可求得P的坐标.
(2)先求出直线DE的斜率,设直线DE的解析式是y=
| 3 |
(3)分当FM是菱形的边和当OF是对角线两种情况进行讨论.利用三角函数即可求得P的坐标.
解答:解:(1)在直角△OAC中,
∵∠ACO=30°
∴tan∠ACO=
=
,
∴设OA=
x,则OC=3x,
根据勾股定理得:(3x)2+(
x)2=AC2,
即9x2+3x2=144,
解得:x=2
.
故C的坐标是:(6
,0),B的坐标是(6
,6);
(2)∵直线AC的斜率是:-
=-
,
∴直线DE的斜率是:
.
∴设直线DE的解析式是y=
x+b,
∵G(0,-6),
∴b=-6,
∴直线DE的解析式是:y=
x-6;
(3)∵C的坐标是:(6
,0),B的坐标是(6
,6);
∴A(0,6),
∴设直线AC的解析式为y=kx+b(k≠0),
∴
,
解得
.
∴直线AC的解析式为y=-
x+6.
∵直线DE的解析式为y=
x-6,
∴
,
解得
.
∴F是线段AC的中点,
∴OF=
AC=6,
∵直线DE的斜率是:
.
∴DE与x轴夹角是60°,
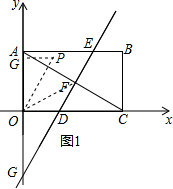
当FM是菱形的边时(如图1),ON∥FM,
则∠POC=60°或120°.
当∠POC=60°时,过N作NG⊥y轴,则PG=OP•sin30°=6×
=3,
OG=OP•cos30°=6×
=3
,则P的坐标是(3,3
);
当∠NOC=120°时,与当∠POC=60°时关于原点对称,则坐标是(-3,-3
);
当OF是对角线时(如图2),MP关于OF对称.
∵F的坐标是(3
,3),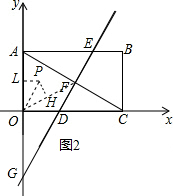
∴∠FOD=∠POF=30°,
在直角△OPH中,OH=
OF=3,OP=
=
=2
.
作PL⊥y轴于点L.
在直角△OPL中,∠POL=30°,
则PL=
OP=
,
OL=OP•cos30°=2
×
=3.
故P的坐标是(
,3).
当DE与y轴的交点时G,这个时候P在第四象限,
此时点的坐标为:(3
,-3).
则P的坐标是:(3
,-3)或(3,3
)或(-3,-3
)或(
,3).
∵∠ACO=30°
∴tan∠ACO=
| OA |
| OC |
| ||
| 3 |
∴设OA=
| 3 |
根据勾股定理得:(3x)2+(
| 3 |
即9x2+3x2=144,
解得:x=2
| 3 |
故C的坐标是:(6
| 3 |
| 3 |
(2)∵直线AC的斜率是:-
| 6 | ||
6
|
| ||
| 3 |
∴直线DE的斜率是:
| 3 |
∴设直线DE的解析式是y=
| 3 |
∵G(0,-6),
∴b=-6,
∴直线DE的解析式是:y=
| 3 |
(3)∵C的坐标是:(6
| 3 |
| 3 |
∴A(0,6),
∴设直线AC的解析式为y=kx+b(k≠0),
∴
|
解得
|
∴直线AC的解析式为y=-
| ||
| 3 |
∵直线DE的解析式为y=
| 3 |
∴
|
解得
|
∴F是线段AC的中点,
∴OF=
| 1 |
| 2 |
∵直线DE的斜率是:
| 3 |

∴DE与x轴夹角是60°,
当FM是菱形的边时(如图1),ON∥FM,
则∠POC=60°或120°.
当∠POC=60°时,过N作NG⊥y轴,则PG=OP•sin30°=6×
| 1 |
| 2 |
OG=OP•cos30°=6×
| ||
| 2 |
| 3 |
| 3 |
当∠NOC=120°时,与当∠POC=60°时关于原点对称,则坐标是(-3,-3
| 3 |
当OF是对角线时(如图2),MP关于OF对称.
∵F的坐标是(3
| 3 |

∴∠FOD=∠POF=30°,
在直角△OPH中,OH=
| 1 |
| 2 |
| OH |
| cos∠POH |
| 3 | ||||
|
| 3 |
作PL⊥y轴于点L.
在直角△OPL中,∠POL=30°,
则PL=
| 1 |
| 2 |
| 3 |
OL=OP•cos30°=2
| 3 |
| ||
| 2 |
故P的坐标是(
| 3 |
当DE与y轴的交点时G,这个时候P在第四象限,
此时点的坐标为:(3
| 3 |
则P的坐标是:(3
| 3 |
| 3 |
| 3 |
| 3 |
点评:本题考查了一次函数综合题,在解答(3)时要注意分两种情况进行讨论,不要漏解.

练习册系列答案
 世纪百通期末金卷系列答案
世纪百通期末金卷系列答案
相关题目

 如图,一个圆柱,它的高为20cm,底面半径为7cm.如果一只蚂蚁要自圆柱下底面的A点,沿圆柱体的侧面爬到与A相对的上底面B点,求爬行的最短长度(结果保留π).
如图,一个圆柱,它的高为20cm,底面半径为7cm.如果一只蚂蚁要自圆柱下底面的A点,沿圆柱体的侧面爬到与A相对的上底面B点,求爬行的最短长度(结果保留π). 如图,在直角梯形ABCD中,AD∥BC,∠BAD=90°,AB=4,CD=5,AD=6,动点P从点A开始以每秒1个单位长度的速度向点B匀速运动,动点Q从点B开始沿折线BC-CD以每秒2个单位长度的速度向点D匀速运动,过点P作PE⊥AB,交CD于点E,设点P、Q同时开始运动,且时间为t秒(t>0),当点P与点B重合时停止运动,点Q也随之停止运动.
如图,在直角梯形ABCD中,AD∥BC,∠BAD=90°,AB=4,CD=5,AD=6,动点P从点A开始以每秒1个单位长度的速度向点B匀速运动,动点Q从点B开始沿折线BC-CD以每秒2个单位长度的速度向点D匀速运动,过点P作PE⊥AB,交CD于点E,设点P、Q同时开始运动,且时间为t秒(t>0),当点P与点B重合时停止运动,点Q也随之停止运动.