题目内容
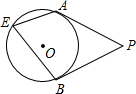 如图,PA,PB分别切⊙O于点A,B,点E是⊙O上一点,且∠AEB=50°,则∠P=
如图,PA,PB分别切⊙O于点A,B,点E是⊙O上一点,且∠AEB=50°,则∠P=考点:切线的性质
专题:计算题
分析:连接OA、OB,如图,根据切线的性质得OA⊥AP,OB⊥AB,则∠PAO=∠PBO=90°,利用四边形的内角和得到∠P+∠AOB=180°,然后根据圆周角定理得到
∠AOB的度数,再利用互补计算∠P的度数.
∠AOB的度数,再利用互补计算∠P的度数.
解答:解: 连接OA、OB,如图,
连接OA、OB,如图,
∵PA、PB分别切⊙O于A、B两点,
∴OA⊥AP,OB⊥AB,
∴∠PAO=∠PBO=90°,
∴∠P+∠AOB=180°,
∵∠AOB=2∠AEB=2×50°=100°,
∴∠P=180°-100°=80°.
故答案为80°.
 连接OA、OB,如图,
连接OA、OB,如图,∵PA、PB分别切⊙O于A、B两点,
∴OA⊥AP,OB⊥AB,
∴∠PAO=∠PBO=90°,
∴∠P+∠AOB=180°,
∵∠AOB=2∠AEB=2×50°=100°,
∴∠P=180°-100°=80°.
故答案为80°.
点评:本题考查了切线的性质:圆的切线垂直于经过切点的半径.也考查了圆周角定理.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
设[x]表示不超过x的最大整数,如[2.7]=2,[-4.5]=-5;计算[3.7]+[-6.5]的值为( )
| A、-2 | B、-3 | C、-4 | D、3 |
 如图,一个圆柱,它的高为20cm,底面半径为7cm.如果一只蚂蚁要自圆柱下底面的A点,沿圆柱体的侧面爬到与A相对的上底面B点,求爬行的最短长度(结果保留π).
如图,一个圆柱,它的高为20cm,底面半径为7cm.如果一只蚂蚁要自圆柱下底面的A点,沿圆柱体的侧面爬到与A相对的上底面B点,求爬行的最短长度(结果保留π). 如图,在直角梯形ABCD中,AD∥BC,∠BAD=90°,AB=4,CD=5,AD=6,动点P从点A开始以每秒1个单位长度的速度向点B匀速运动,动点Q从点B开始沿折线BC-CD以每秒2个单位长度的速度向点D匀速运动,过点P作PE⊥AB,交CD于点E,设点P、Q同时开始运动,且时间为t秒(t>0),当点P与点B重合时停止运动,点Q也随之停止运动.
如图,在直角梯形ABCD中,AD∥BC,∠BAD=90°,AB=4,CD=5,AD=6,动点P从点A开始以每秒1个单位长度的速度向点B匀速运动,动点Q从点B开始沿折线BC-CD以每秒2个单位长度的速度向点D匀速运动,过点P作PE⊥AB,交CD于点E,设点P、Q同时开始运动,且时间为t秒(t>0),当点P与点B重合时停止运动,点Q也随之停止运动.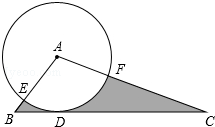 如图,在△ABC中,BC=6,以点A为圆心,2为半径的⊙A与BC相切于点D,交AB于点E,交AC于点F,∠EAF=120°,则图中阴影部分的面积是
如图,在△ABC中,BC=6,以点A为圆心,2为半径的⊙A与BC相切于点D,交AB于点E,交AC于点F,∠EAF=120°,则图中阴影部分的面积是