题目内容
 如图,已知在△ADC中,∠C=90°,AB⊥AC,D、E、B在一直线上,BE=2AD,求证:∠ADE=2∠EDC.
如图,已知在△ADC中,∠C=90°,AB⊥AC,D、E、B在一直线上,BE=2AD,求证:∠ADE=2∠EDC.考点:直角三角形斜边上的中线
专题:
分析:取BE的中点M,连接AM,根据直角三角形斜边上中线性质求出BE=2AAM,求出AM=AD,推出∠ADE=∠AME,求出∠AME=2∠B=2∠EDC,即可得出答案.
解答:证明:
取BE的中点M,连接AM,
∵AB⊥AC,
∴∠BAE=90°,
∴AM=BM=ME,
∴∠B=∠BAM,
∴∠AME=∠B+∠BAM=2∠B,
∵AM=BM=ME,
∴BE=2AM,
∵BE=2AD,
∴AD=AM,
∴∠ADB=∠AMD=2∠B,
∵∠BAE=∠C=90°,
∴∠EDC=∠B,
∴∠ADE=2∠EDC.

取BE的中点M,连接AM,
∵AB⊥AC,
∴∠BAE=90°,
∴AM=BM=ME,
∴∠B=∠BAM,
∴∠AME=∠B+∠BAM=2∠B,
∵AM=BM=ME,
∴BE=2AM,
∵BE=2AD,
∴AD=AM,
∴∠ADB=∠AMD=2∠B,
∵∠BAE=∠C=90°,
∴∠EDC=∠B,
∴∠ADE=2∠EDC.
点评:本题考查了平行线的性质和判定,直角三角形斜边上中线性质,等腰三角形的性质,三角形的外角性质的应用,主要考查学生综合运用性质进行推理的能力.

练习册系列答案
 同步奥数系列答案
同步奥数系列答案
相关题目
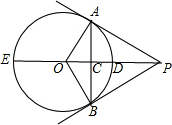 如图,PA、PB是⊙O的切线,切点分别为A、B,直线OP交⊙O于点D、E,交AB于点C.
如图,PA、PB是⊙O的切线,切点分别为A、B,直线OP交⊙O于点D、E,交AB于点C. 已知x2=3,那么在数轴上与实数x对应的点可能是
已知x2=3,那么在数轴上与实数x对应的点可能是
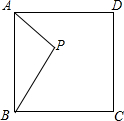 P为正方形ABCD内一点,且AP=2,将△APB绕点A按逆时针方向旋转90°得到△AP′D.
P为正方形ABCD内一点,且AP=2,将△APB绕点A按逆时针方向旋转90°得到△AP′D. 如图,一个圆柱,它的高为20cm,底面半径为7cm.如果一只蚂蚁要自圆柱下底面的A点,沿圆柱体的侧面爬到与A相对的上底面B点,求爬行的最短长度(结果保留π).
如图,一个圆柱,它的高为20cm,底面半径为7cm.如果一只蚂蚁要自圆柱下底面的A点,沿圆柱体的侧面爬到与A相对的上底面B点,求爬行的最短长度(结果保留π).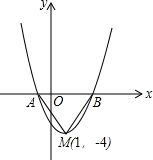 如图是二次函数y=(x+m)2+k的图象,其顶点坐标为M(1,-4).
如图是二次函数y=(x+m)2+k的图象,其顶点坐标为M(1,-4).