题目内容
13.在平面直角坐标系中,已知A($\sqrt{3}$,1),B(2,0),O(0,0),反比例函数y=$\frac{k}{x}$的图象经过点A.(1)求k的值;
(2)将△AOB绕点O逆时针旋转60°,得到△COD,其中点A与点C对应,点B与点D对应,试判断点D是否在该反比例函数的图象上.
分析 (1)根据反比例函数y=$\frac{k}{x}$的图象经过点A($\sqrt{3}$,1),可以求得k的值;
(2)根据题目中信息可以画出旋转后的图形,然后求出点D的坐标,即可判断点D是否在该函数的图象上,本题得以解决.
解答 解:(1)∵反比例函数y=$\frac{k}{x}$的图象经过点A($\sqrt{3}$,1),
∴$1=\frac{k}{\sqrt{3}}$,得k=$\sqrt{3}$,
即k的值是$\sqrt{3}$;
(2)∵B(2,0)
∴OB=2
又∵△AOB绕点O逆时针旋转60°得到△COD
∴OD=OB=2,∠BOD=60°,
如右图所示,过点D作DE⊥x轴于点E,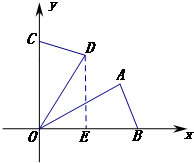 在Rt△DOE中,
在Rt△DOE中,
OE=OD•cos60°=$2×\frac{1}{2}=1$,DE=OD•sin60°=$2×\frac{\sqrt{3}}{2}=\sqrt{3}$,
∴D点坐标是(1,$\sqrt{3}$),
由(1)知,反比例函数的解析式$y=\frac{\sqrt{3}}{x}$,
当x=1时,$y=\sqrt{3}$,
∴点D(1,$\sqrt{3}$)在该反比例函的图象上.
点评 本题考查反比例函数图象上点的坐标特征、坐标与图形的变化-旋转,解题的关键是明确题意,画出相应的图形,求出相应的函数解析式和点的坐标,

练习册系列答案
 出彩同步大试卷系列答案
出彩同步大试卷系列答案
相关题目
3.矩形ABCD的对角线AC,BD相交于点O,∠AOD=120°,AC=6,则△ABO的周长为( )
| A. | 18 | B. | 15 | C. | 12 | D. | 9 |
1.下列汽车标志中,可以看作中心对称图形的是( )
| A. |  | B. |  | C. |  | D. |  |
18.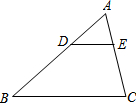 如图,在△ABC中,D、E分别是AB、AC上的点,且DE∥BC,若DE=2,BC=5,则AD:DB=( )
如图,在△ABC中,D、E分别是AB、AC上的点,且DE∥BC,若DE=2,BC=5,则AD:DB=( )
 如图,在△ABC中,D、E分别是AB、AC上的点,且DE∥BC,若DE=2,BC=5,则AD:DB=( )
如图,在△ABC中,D、E分别是AB、AC上的点,且DE∥BC,若DE=2,BC=5,则AD:DB=( )| A. | 3:2 | B. | 3:5 | C. | 2:5 | D. | 2:3 |
3.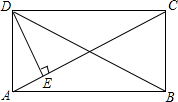 已知:如图,在矩形ABCD中,DE⊥AC,∠ADE=$\frac{1}{3}$∠CDE,那么∠BDC等于( )
已知:如图,在矩形ABCD中,DE⊥AC,∠ADE=$\frac{1}{3}$∠CDE,那么∠BDC等于( )
 已知:如图,在矩形ABCD中,DE⊥AC,∠ADE=$\frac{1}{3}$∠CDE,那么∠BDC等于( )
已知:如图,在矩形ABCD中,DE⊥AC,∠ADE=$\frac{1}{3}$∠CDE,那么∠BDC等于( )| A. | 60° | B. | 45° | C. | 30° | D. | 22.5° |
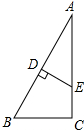 如图,在Rt△ABC中,∠C=90°,∠A=30°,∠ABC=60°,AB的垂直平分线分别交AB,AC于点D,E.
如图,在Rt△ABC中,∠C=90°,∠A=30°,∠ABC=60°,AB的垂直平分线分别交AB,AC于点D,E.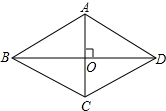 如图,四边形ABCD是菱形,对角线AC与BD相交于点O,AC=24,BD=10,求菱形ABCD的周长.
如图,四边形ABCD是菱形,对角线AC与BD相交于点O,AC=24,BD=10,求菱形ABCD的周长.