题目内容
15.已知$\frac{2a+5}{{a}^{2}-5a+6}$=$\frac{A}{a-2}$+$\frac{B}{a-3}$,求2A+B的值.分析 已知等式右边通分并利用同分母分式的加法法则计算,再利用分式相等的条件求出A与B的值,代入原式计算即可得到结果.
解答 解:已知等式整理得:$\frac{2a+5}{{a}^{2}-5a+6}$=$\frac{A(a-3)+B(a-2)}{(a-2)(a-3)}$=$\frac{(A+B)a-3A-2B}{{a}^{2}-5a+6}$,
可得2a+5=(A+B)a-3A-2B,
∴$\left\{\begin{array}{l}{A+B=2}\\{-3A-2B=5}\end{array}\right.$,
解得:$\left\{\begin{array}{l}{A=-9}\\{B=11}\end{array}\right.$,
则2A+B=-18+11=-7.
点评 此题考查了分式的加减法,熟练掌握运算法则是解本题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
18.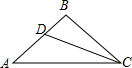 如图,在△ABC中,∠A=∠ACB,CD平分∠ACB交AB于点D,∠ADC=150°,则∠B为( )
如图,在△ABC中,∠A=∠ACB,CD平分∠ACB交AB于点D,∠ADC=150°,则∠B为( )
 如图,在△ABC中,∠A=∠ACB,CD平分∠ACB交AB于点D,∠ADC=150°,则∠B为( )
如图,在△ABC中,∠A=∠ACB,CD平分∠ACB交AB于点D,∠ADC=150°,则∠B为( )| A. | 120° | B. | 130° | C. | 140° | D. | 150° |
 如图,已知等边△ABC,延长BC至D,E在AB上,使AE=CD,连接DE,交AC于F点,过E作EG⊥AC于G点.求证:FG=$\frac{1}{2}$AC.
如图,已知等边△ABC,延长BC至D,E在AB上,使AE=CD,连接DE,交AC于F点,过E作EG⊥AC于G点.求证:FG=$\frac{1}{2}$AC. 根据立体图从上面看到的形状图(如图所示),画出它从正面和左面看到的形状图(图中数字代表该位置的小正方体的个数).
根据立体图从上面看到的形状图(如图所示),画出它从正面和左面看到的形状图(图中数字代表该位置的小正方体的个数).