题目内容
18.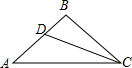 如图,在△ABC中,∠A=∠ACB,CD平分∠ACB交AB于点D,∠ADC=150°,则∠B为( )
如图,在△ABC中,∠A=∠ACB,CD平分∠ACB交AB于点D,∠ADC=150°,则∠B为( )| A. | 120° | B. | 130° | C. | 140° | D. | 150° |
分析 由角的平分线的性质得到∠ACD=$\frac{1}{2}$∠ACB,再由三角形的内角和定理建立方程,求得∠ACB的度数,进而求得∠B的度数.
解答 解:∵CD平分∠ACB,
∴∠ACD=$\frac{1}{2}$∠ACB,
∵∠A=∠ACB,
∴∠B=180°-2∠ACB,
∵∠BDC=∠A+∠ACD=150°,
∴180°-2∠ACB+$\frac{1}{2}$∠ACB=150°,
∴∠ACB=20°,
∴∠B=140°,
故选:C.
点评 本题考查了等腰三角形的性质,角的平分线的性质,三角形内角和定理.找着各角的关系利用三角形内角和定理求解是正确解答本题的关键.

练习册系列答案
相关题目
10.下列不等式中,正确的是( )
| A. | $-4\frac{2}{3}>-4.7$ | B. | $-\frac{12}{23}<-\frac{6}{11}$ | C. | -0.2<-0.22 | D. | $-0.01<-\frac{1}{100}$ |
7.下列各组线段能成比例的是( )
| A. | 0.2cm 0.3m 0.4cm 0.2cm | B. | 1cm 2cm 3cm 4cm | ||
| C. | 4cm 6cm 8cm 3cm | D. | $\sqrt{2}$cm $\sqrt{6}$cm $\sqrt{8}$cm $\sqrt{7}$cm |

 如图,直线AB、CD相交于点O,OE⊥AB,∠EOD=20°,∠AOC=70°.
如图,直线AB、CD相交于点O,OE⊥AB,∠EOD=20°,∠AOC=70°. 如图,已知⊙O的半径为6cm,射线PM经过点O,OP=10cm,射线PN与⊙O相切于点Q.A、B两点同时从点P出发,点A以5cm/s的速度沿射线PM方向运动,点B以4cm/s的速度沿射线PN方向运动,设运动时间为t s.
如图,已知⊙O的半径为6cm,射线PM经过点O,OP=10cm,射线PN与⊙O相切于点Q.A、B两点同时从点P出发,点A以5cm/s的速度沿射线PM方向运动,点B以4cm/s的速度沿射线PN方向运动,设运动时间为t s.