题目内容
5. 如图,已知等边△ABC,延长BC至D,E在AB上,使AE=CD,连接DE,交AC于F点,过E作EG⊥AC于G点.求证:FG=$\frac{1}{2}$AC.
如图,已知等边△ABC,延长BC至D,E在AB上,使AE=CD,连接DE,交AC于F点,过E作EG⊥AC于G点.求证:FG=$\frac{1}{2}$AC.
分析 延长GA到点H,使AH=FC,连接HE,可证明△AHE≌△CFD,可知∠H=∠CFD,结合对顶角可证得EA=EF,可知HG=GF,可证得结论.
解答 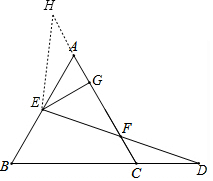 证明:
证明:
如图,延长GA到点H,使AH=FC,连接HE,
∵△ABC为等边三角形,
∴∠BAC=∠ACB=60°,
∴∠HAE=∠FCD=120°,
在△AHE和△CFD中
$\left\{\begin{array}{l}{AE=CD}\\{∠HAE=∠FCD}\\{AH=CF}\end{array}\right.$
∴△AHE≌△CFD(SAS),
∴∠EHA=∠CFD=∠GFE,
∴EH=EF,
∵EG⊥AC,
∴EG=GF,
∵HG=HA+AG=AG+FC,
∴AG+FC=GF,
∴FG=$\frac{1}{2}$AC.
点评 本题主要考查等边三角形的性质及全等三角形的判定和性质,构造三角形全等是解题的关键.

练习册系列答案
相关题目
16.现定义运算“★”,对于任意实数a,b,都有a★b=a2-a×b+b,如:3★5=32-3×5+5,若x★2=10,则实数x的值为( )
| A. | -4或-l | B. | 4或-l | C. | 4或-2 | D. | -4或2 |

 如图,抛物线y=-$\frac{2}{3}$x2+bx+c经过A(-1,0),B(0,2)两点,将△OAB绕点B逆时针旋转90°后得到△O′A′B′,点A落到点A′的位置.
如图,抛物线y=-$\frac{2}{3}$x2+bx+c经过A(-1,0),B(0,2)两点,将△OAB绕点B逆时针旋转90°后得到△O′A′B′,点A落到点A′的位置. 有两部不同型号的手机(分别记为A、B)和与之匹配的2个保护盖(分别记为a、b)(如图所示)散乱地放在桌子上,若从手机和保护盖中随机取两个,用树形图法或列表法,求恰好匹配的概率.
有两部不同型号的手机(分别记为A、B)和与之匹配的2个保护盖(分别记为a、b)(如图所示)散乱地放在桌子上,若从手机和保护盖中随机取两个,用树形图法或列表法,求恰好匹配的概率.