题目内容
9. 如图所示,点A的坐标为A(0,a),将点A向右平移b个单位得到点B,其中a,b满足:(3a-2b)2+|a+b-5|=0.
如图所示,点A的坐标为A(0,a),将点A向右平移b个单位得到点B,其中a,b满足:(3a-2b)2+|a+b-5|=0.(1)求点B的坐标并求△AOB的面积S△AOB;
(2)在x轴上是否存在一点D,使得S△AOB=2S△AOD?若存在,求出D点的坐标;若不存在,说明理由.
分析 (1)根据非负数的性质求得a,b即可;
(2)设D(x,0),根据S△AOB=2S△AOD即可求得x的长,进而求得D的坐标.
解答 解:(1)∵(3a-2b)2+|a+b-5|=0,
∴$\left\{\begin{array}{l}{3a-2b=0}\\{a+b-5=0}\end{array}\right.$,
解得:$\left\{\begin{array}{l}{a=3}\\{b=2}\end{array}\right.$,
∴B(3,2);
S△AOB=$\frac{1}{2}$×2×(3-0)=3;
(2)设D(x,0),
∵S△AOB=2S△AOD,
∴2×$\frac{1}{2}$×2|x|=3,
解得:x=-$\frac{3}{2}$,或$\frac{3}{2}$,
D为(-$\frac{3}{2}$,0)或($\frac{3}{2}$,0).
点评 本题主要考查了点的坐标的平移,非负数的性质三角形的面积公式,能够分类求解是解题的关键.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
8.下列函数中有最小值的是( )
| A. | y=2x-1 | B. | y=-$\frac{3}{x}$ | C. | y=2x2+3x | D. | y=-x2+1 |
17. 下列选项中,能由图1平移得到的是( )
下列选项中,能由图1平移得到的是( )
 下列选项中,能由图1平移得到的是( )
下列选项中,能由图1平移得到的是( )| A. |  | B. |  | C. |  | D. |  |
 如图,在三角形ABC中,BC=8,将三角形ABC以每秒2cm的速度沿BC所在直线向右平移,所得图形对应为三角形DEF,设平移的时间为t秒,当t=8时,AD=2CE.
如图,在三角形ABC中,BC=8,将三角形ABC以每秒2cm的速度沿BC所在直线向右平移,所得图形对应为三角形DEF,设平移的时间为t秒,当t=8时,AD=2CE.
 如图,矩形OABC的两条边在坐标轴上,OA=1,OC=2,现将此矩形向右平移1个单位,若平移后得到的矩形的边与反比例函数y=$\frac{k}{x}$图象有两个交点,它们的纵坐标之差的绝对值为0.6,则k的值为$\frac{14}{5}$或$\frac{6}{5}$.
如图,矩形OABC的两条边在坐标轴上,OA=1,OC=2,现将此矩形向右平移1个单位,若平移后得到的矩形的边与反比例函数y=$\frac{k}{x}$图象有两个交点,它们的纵坐标之差的绝对值为0.6,则k的值为$\frac{14}{5}$或$\frac{6}{5}$. 在如图所示的直角坐标系中,每个小方格都是边长为1的正方形,△ABC的顶点均在格点上,点A的坐标 是(-3,-1).将△ABC沿y轴正方向平移3个单位得到△A1B1C1,画出△A1B1C1,并写出点B1的坐标.
在如图所示的直角坐标系中,每个小方格都是边长为1的正方形,△ABC的顶点均在格点上,点A的坐标 是(-3,-1).将△ABC沿y轴正方向平移3个单位得到△A1B1C1,画出△A1B1C1,并写出点B1的坐标.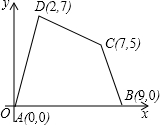 如图,已知四边形ABCD四个顶点的坐标分别为A(0,0),B(9,0),C(7,5),D(2,7).将该四边形先向右平移2个单位,再向下平移3个单位后得到四边形A1B1C1D1,求四边形A1B1C1D1的面积.
如图,已知四边形ABCD四个顶点的坐标分别为A(0,0),B(9,0),C(7,5),D(2,7).将该四边形先向右平移2个单位,再向下平移3个单位后得到四边形A1B1C1D1,求四边形A1B1C1D1的面积.