题目内容
7.方程x4-x2-6=0,设y=x2,则原方程变形为y2-y-6=0,原方程的根为x1=$\sqrt{3}$,x2=$-\sqrt{3}$.分析 根据题意可以得到变形后的方程,然后根据解一元二次方程的方法即可求得x的值.
解答 解:∵方程x4-x2-6=0,设y=x2,
∴原方程变形为:y2-y-6=0,
∴(y-3)(y+2)=0,
∴y1=3,y2=-2(舍去),
∴x2=3,
得x1=$\sqrt{3}$,x2=$-\sqrt{3}$,
故答案为:y2-y-6=0,x1=$\sqrt{3}$,x2=$-\sqrt{3}$.
点评 本题考查换元法解一元二次方程,解答本题的关键是明确换元法解一元二次方程的方法.

练习册系列答案
相关题目
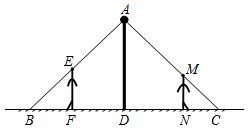 如图,小强和小华共同站在路灯下,小强的身高EF=1.8m,小华的身高MN=1.5m,他们的影子恰巧等于自己的身高,即BF=1.8m,CN=1.5m,且两人相距4.7m,则路灯AD的高度是4m.
如图,小强和小华共同站在路灯下,小强的身高EF=1.8m,小华的身高MN=1.5m,他们的影子恰巧等于自己的身高,即BF=1.8m,CN=1.5m,且两人相距4.7m,则路灯AD的高度是4m.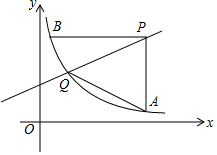 如图,直线y=$\frac{1}{2}$x+m与反比例函数y=$\frac{k}{x}$(x>0)的图象交于Q点,点B(1,6)在反比例函数的图象上,过B作BP∥x轴交直线y=$\frac{1}{2}$x+m于点P,过点P作PA∥y轴交双曲线于点A,连结AQ,BQ.
如图,直线y=$\frac{1}{2}$x+m与反比例函数y=$\frac{k}{x}$(x>0)的图象交于Q点,点B(1,6)在反比例函数的图象上,过B作BP∥x轴交直线y=$\frac{1}{2}$x+m于点P,过点P作PA∥y轴交双曲线于点A,连结AQ,BQ. 如图,直线y=mx与y=-$\frac{1}{x}$和y=$\frac{k}{x}$分别交于A,B两点,且OB=2OA,则k=-4.
如图,直线y=mx与y=-$\frac{1}{x}$和y=$\frac{k}{x}$分别交于A,B两点,且OB=2OA,则k=-4.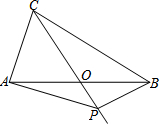 如图,在△ABC中,AB=BC=6,AO=BO,P是射线CO上的一个动点,∠AOC=60°,则当△PAB为直角三角形时,sin∠PAB=$\frac{1}{2}$或$\frac{\sqrt{21}}{7}$或$\frac{\sqrt{3}}{2}$.
如图,在△ABC中,AB=BC=6,AO=BO,P是射线CO上的一个动点,∠AOC=60°,则当△PAB为直角三角形时,sin∠PAB=$\frac{1}{2}$或$\frac{\sqrt{21}}{7}$或$\frac{\sqrt{3}}{2}$.