题目内容
12. 如图,直线y=mx与y=-$\frac{1}{x}$和y=$\frac{k}{x}$分别交于A,B两点,且OB=2OA,则k=-4.
如图,直线y=mx与y=-$\frac{1}{x}$和y=$\frac{k}{x}$分别交于A,B两点,且OB=2OA,则k=-4.
分析 作AC⊥x轴于点C,作BD⊥x轴于点D,则△OBD∽△OAC,求得△OBD的面积,利用反比例函数比例系数k的几何意义求解.
解答 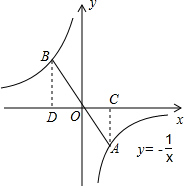 解:作AC⊥x轴于点C,作BD⊥x轴于点D.
解:作AC⊥x轴于点C,作BD⊥x轴于点D.
则BD∥AC,△OBD∽△OAC.
∵A在y=-$\frac{1}{x}$上,
∴S△OAC=$\frac{1}{2}$.
∴$\frac{{S}_{△OBD}}{{S}_{△OAC}}$=($\frac{OB}{OA}$)2=4,
∴S△OBD=4×$\frac{1}{2}$=2,
∴k=-4.
点评 本题考查了相似三角形的判定与性质以及反比例函数的比例系数k的几何意义,在反比例函数的图象上任意一点向坐标轴作垂线,这一点和垂足以及坐标原点所构成的三角形的面积是$\frac{1}{2}$|k|,且保持不变.

练习册系列答案
 七星图书口算速算天天练系列答案
七星图书口算速算天天练系列答案
相关题目
7.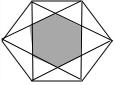 如图,边长为a的正六边形中,连接一些顶点,中间围成一个新的小正六边形(阴影部分),则$\frac{{l}_{外部正六边形}}{{l}_{阴影}}$(l为周长)等于( )
如图,边长为a的正六边形中,连接一些顶点,中间围成一个新的小正六边形(阴影部分),则$\frac{{l}_{外部正六边形}}{{l}_{阴影}}$(l为周长)等于( )
 如图,边长为a的正六边形中,连接一些顶点,中间围成一个新的小正六边形(阴影部分),则$\frac{{l}_{外部正六边形}}{{l}_{阴影}}$(l为周长)等于( )
如图,边长为a的正六边形中,连接一些顶点,中间围成一个新的小正六边形(阴影部分),则$\frac{{l}_{外部正六边形}}{{l}_{阴影}}$(l为周长)等于( )| A. | 3 | B. | $\sqrt{3}$ | C. | $\frac{\sqrt{3}}{3}$ | D. | 2 |
17.下列说法正确的是( )
| A. | 若|a|=-a,则a<0 | B. | 若a<0,ab<0,则b>0 | ||
| C. | 若ab>0,则a>0,b>0 | D. | 若a=b,m是有理数,则$\frac{a}{m}$=$\frac{b}{m}$ |