题目内容
2．“一个角一定不等于它的补角”这个命题正确吗？若正确请说明理由，若不正确，请举反例．分析 根据补角的性质举出反例即可判定该命题是假命题；
解答 解：“一个角一定不等于它的补角”这个命题不正确；
反例：90°的补角等于90°，二者相等．
点评 本题考查了命题与定理的知识，解题的关键是了解补角的定义及性质，难度不大．
练习册系列答案
相关题目
如图．在正方形ABCD中，点P是BC延长线上一点，BQ⊥PD于点Q，QN⊥BD于点N，连接AN．若S△DMQ=$\frac{1}{8}$DM2，AB=4，则AN的长为$\sqrt{10}$．
7．
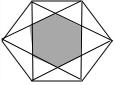如图，边长为a的正六边形中，连接一些顶点，中间围成一个新的小正六边形（阴影部分），则$\frac{{l}_{外部正六边形}}{{l}_{阴影}}$（l为周长）等于（ ）
如图，边长为a的正六边形中，连接一些顶点，中间围成一个新的小正六边形（阴影部分），则$\frac{{l}_{外部正六边形}}{{l}_{阴影}}$（l为周长）等于（ ）| A． | 3 | B． | $\sqrt{3}$ | C． | $\frac{\sqrt{3}}{3}$ | D． | 2 |
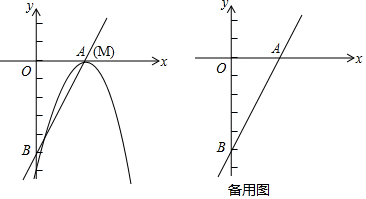
14．
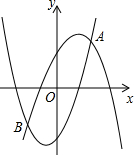如图，抛物线y1=a（x+1）2-5与抛物线y2=-a（x-1）2+5（a≠0）的交点A，B，点A，B的坐标分别是（2，4），（m，-4），若无论x取何值，y总取y1，y2中的最小值．则y的最大值是（ ）
如图，抛物线y1=a（x+1）2-5与抛物线y2=-a（x-1）2+5（a≠0）的交点A，B，点A，B的坐标分别是（2，4），（m，-4），若无论x取何值，y总取y1，y2中的最小值．则y的最大值是（ ）| A． | 5 | B． | 4 | C． | 2 | D． | 1 |
8．以40m/s的速度将小球沿与地面成30°角的方向击出时，球的飞行路线将是一条抛物线．如果不考虑空气阻力，球的飞行高度h（米）与飞行时间t（秒）的关系如下表，且h与t的函数关系是我们学过的一次函数、二次函数、反比例函数中的一种
（1）请你从上述函数中选择一种合适的函数，求出它的函数关系式，并简要说明不选择另外两种函数的理由
（2）什么时候小球最高？最大高度是多少？
（3）小球运动的时间t在什么范围内，小球在运动过程中的高度不低于18.75米．
| 时间t（秒） | 0 | 1 | 3 | 4 |
| 高度h（米） | 0 | 15 | 15 | 0 |
（2）什么时候小球最高？最大高度是多少？
（3）小球运动的时间t在什么范围内，小球在运动过程中的高度不低于18.75米．